Operations Management - Transportation / Assignment & Inventory Management
Introduction of Assignment Problems
Posted On :
Assignment problems are special case of linear programming problems. The task is to assign ‘i’ resources (i= 1, 2, 3, 4 …m) to ‘j’ tasks (j= 1, 2, 3, 4…n) in such a way that the total cost of performing the tasks is lowest.
Introduction of Assignment Problems
Assignment problems are special case of linear programming problems. The task is to assign ‘i’ resources (i= 1, 2, 3, 4 …m) to ‘j’ tasks (j= 1, 2, 3, 4…n) in such a way that the total cost of performing the tasks is lowest. The cost associated in performing resource-i by task-j is denoted by ‘Cij’. Moreover, each resource should be exactly performed by one task. Thus, the assignment problem is a special type of Linear Programming Problems, where assignees are being assigned to perform tasks. In general, in the assigning people to jobs is a common application; however, the assignees need not be people; they can also be machines, projects, location or plants.
Classic examples, like assigning the machine operator to the most suitable job, assigning the set of project managers to most suitable projects and assigning the subject to suitable faculty typically fall under the category of assignment problems.
In the machine operator- job assignment, the objective of the firm may be reducing the overall time taken or reducing the wastages by appropriately assigning the operators to the suitable job; in assigning the project managers to suitable projects, the firm may have an objective of reducing the overall lead time, or cost of operation; in the example of subject-faculty allocation, the university education administrator may be interested in reducing the total number of ‘failures’ in a class.
Thus, a typical assignment problem falls under the category of minimization model; of course, maximization models can also be solved by the Assignment algorithms after suitable modifications. The mathematical expression / formulation of the assignment problem shall be written as:
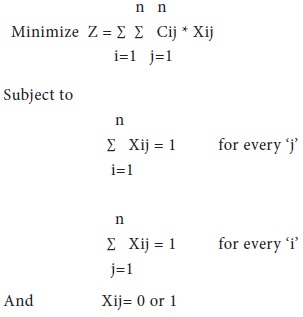
Thus, the assignment problems are zero-one problems, where the decision variables Xij take the value of either zero or one only. The assignment problems can also be consider as special case of ‘Transportation Models’, where, ‘m= n’; that is the number of sources is equal to number of destinations and ai=1 and bj=1 for all ‘i’ and ‘j’ values.
Even though the assignment problems are considered as special case of ‘transportation models’ or ‘linear programming’ models, it is seldom solved by these methods. We use a different algorithm, more efficient algorithm, which is evolved by a group of ‘Hungary’ mathematicians and named after them as ‘Hungarian Algorithm’.
1. The number of assignees and the number of tasks are equal in number.
2. Each assignee is to be assigned to exactly one task.
3. Each task is to be performed by exactly one assignee.
4. There is a cost Cij associated with assignee-i (i= 1, 2, 3 … n) performing a task j (j= 1, 2, 3 … n). This cost can also be estimated with moderate degree of precision always.
5. The
objective is to determine how all the ‘n’ assignments should be made to
minimize the total cost.
Assignment problems are special case of linear programming problems. The task is to assign ‘i’ resources (i= 1, 2, 3, 4 …m) to ‘j’ tasks (j= 1, 2, 3, 4…n) in such a way that the total cost of performing the tasks is lowest. The cost associated in performing resource-i by task-j is denoted by ‘Cij’. Moreover, each resource should be exactly performed by one task. Thus, the assignment problem is a special type of Linear Programming Problems, where assignees are being assigned to perform tasks. In general, in the assigning people to jobs is a common application; however, the assignees need not be people; they can also be machines, projects, location or plants.
Classic examples, like assigning the machine operator to the most suitable job, assigning the set of project managers to most suitable projects and assigning the subject to suitable faculty typically fall under the category of assignment problems.
In the machine operator- job assignment, the objective of the firm may be reducing the overall time taken or reducing the wastages by appropriately assigning the operators to the suitable job; in assigning the project managers to suitable projects, the firm may have an objective of reducing the overall lead time, or cost of operation; in the example of subject-faculty allocation, the university education administrator may be interested in reducing the total number of ‘failures’ in a class.
Thus, a typical assignment problem falls under the category of minimization model; of course, maximization models can also be solved by the Assignment algorithms after suitable modifications. The mathematical expression / formulation of the assignment problem shall be written as:
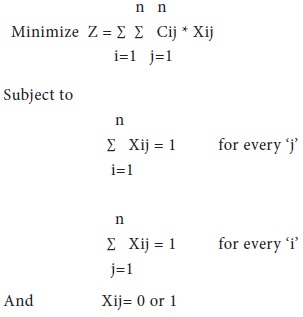
Thus, the assignment problems are zero-one problems, where the decision variables Xij take the value of either zero or one only. The assignment problems can also be consider as special case of ‘Transportation Models’, where, ‘m= n’; that is the number of sources is equal to number of destinations and ai=1 and bj=1 for all ‘i’ and ‘j’ values.
Even though the assignment problems are considered as special case of ‘transportation models’ or ‘linear programming’ models, it is seldom solved by these methods. We use a different algorithm, more efficient algorithm, which is evolved by a group of ‘Hungary’ mathematicians and named after them as ‘Hungarian Algorithm’.
Assumptions in Assignment Problems
1. The number of assignees and the number of tasks are equal in number.
2. Each assignee is to be assigned to exactly one task.
3. Each task is to be performed by exactly one assignee.
4. There is a cost Cij associated with assignee-i (i= 1, 2, 3 … n) performing a task j (j= 1, 2, 3 … n). This cost can also be estimated with moderate degree of precision always.
Tags : Operations Management - Transportation / Assignment & Inventory Management
Last 30 days 1121 views












