Home | ARTS | Operations Management
|
Initial Basic Feasible Solution - Northwest Corner Method - Transportation Problem
Operations Management - Transportation / Assignment & Inventory Management
Initial Basic Feasible Solution - Northwest Corner Method - Transportation Problem
Posted On :
The procedure for constructing an initial basic feasible solution selects the basic variables one at a time.
Initial Basic Feasible Solution - Northwest Corner Method
The procedure for constructing an initial basic feasible solution selects the basic variables one at a time. The North West corner rule, allocation starts to the cell, which occupies the top left-hand corner of the transportation tableau [north-west corner cell / cell- (1, 1)], and proceeds systematically along either a row or a column and make allocations to subsequent cells until the bottom right-hand corner is reached, by which time enough allocations will have been made to constitute an initial solution.
1. Start by selecting the cell in the most \North-West” corner of the table, and set X11 as large as possible (cannot be larger than s1 or d1).
2. Assign the maximum amount to this cell that is allowable based on the requirements and the capacity constraints.
1. If X11 = s1, cross out the first row
[That is exhausting the capacity in the origin].
2. Change d1 to (d1- s1).
[That is modifying the demand after making supply from origin-1 for the market-1].
3. If X11 = d1, cross out the
first column
[That is exhausting the requirements of the market-1].
4. Change s1 to (s1 – d1).
[That is modifying the capacity, after making supply from origin-1 for the market-1].
3. If for any cell, supply equals demand, then the next allocation can be made in cell either in the next row or column; but don’t cross out both the row as well as column. At the row or column, keep a remaining value as zero and make the allocation later to a cell; this will eliminate the process of making dummy basic cells; this issue is called as degeneracy at the initial cell. Degeneracy is reduction in availability of basic cell from the level of (m+n-1).
4. Continue applying procedure to the north-west cell that does not lie in the crossed out row or column until there is one cell left.
We will solve the problem formulated for Adani Power Limited.
Consider the following transportation table.
The north-west corner is cell-(1, 1); the city requirement is 45 and plant-1can supply at most 35.
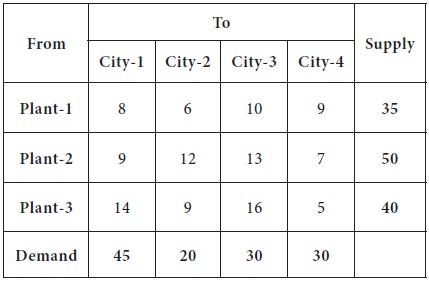
So we decide the supply the entire 35 to city-1;
Now, the plant-1 cannot supply anymore to any cities; and the demand for city-1 will be reduced to 10, after a supply is allocated from plant-1.
This is given in the following table.
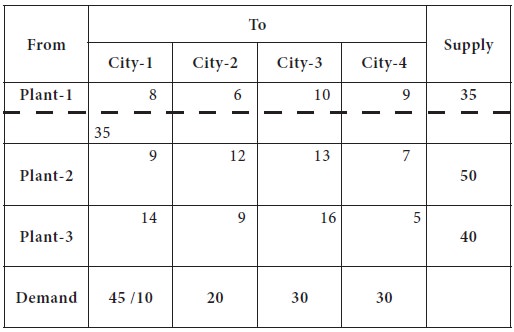
After removing the row-1, again we try to find the north-west corner; this time, it is the cell-(2, 1); the city requirement is 10 and plant-2 can supply at most 50. So we decided to supply the entire requirement of the city-1 [10 units]; now the city-1 requirement is completely fulfilled and removed from further considerations.
And
the availability at plant-2 is reduced to 40 units, after making supply to
city-1. This is given in the following table.
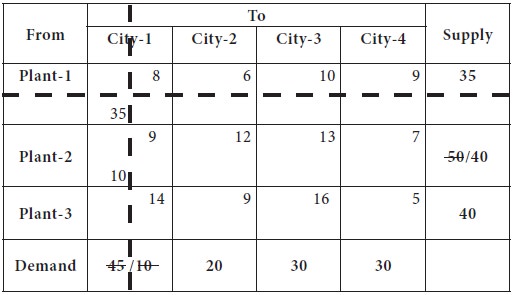
After removing the column-1, again we try to find
the north-west corner; this time, it is the cell-(2, 2); the city-2 requirement
is 20 and plant-2 can supply at most 40. So we decided to supply the entire
requirement of the city-2 [20 units]; now the city-2 requirement is completely
fulfilled and removed from further considerations.
And the availability at plant-2 is reduced to 20 units, after making supply to city-2.
This is given in the following table.
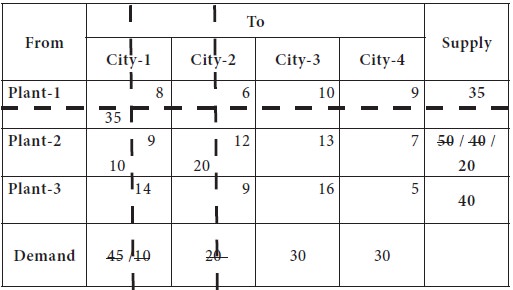
After
removing the column-2, again we try to find the north-west corner; this time,
it is the cell-(2, 3); the city-3 requirement is 30 and plant-2 can supply at
most 20.
So we decided to supply the entire availability at plant-2 [20 units] to the city-3; now the city-2 requirement is reduced to 10 units; however plant-2 is completely exhausted its capacity and hence removed from further considerations.
And the requirement city-3 is reduced to 10 units. This is given in the following table.
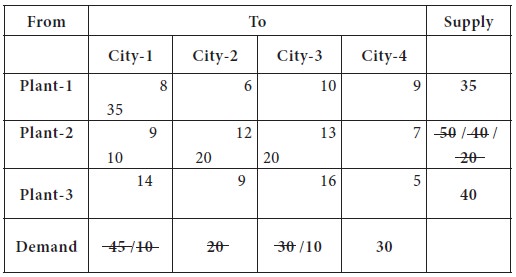
In
the left out table, the north-west corner is cell-(3, 3); the requirement of
the city-3 is 10 units and plant-3 has 40 units with it. Thus the allocation 10
units has been made to cell (3, 3) and left out cell is cell- (3, 4); the
city-4 requirement is 30 units and plant-3 has 30 units left out after
supplying to city-3.
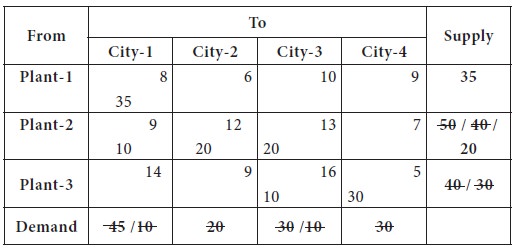
Now the
allocation obtained from north-west corner method is summarized below;
X11 = 35; X21= 10; X22= 20; X23= 20 X33= 10; X34= 30 Total transportation cost through the north-west corner method
TC = (35 X 8) + (10 X 9) + (20 X 12) + (20 X 13) + (10 X 16) + (30 X 5)
= 280 + 90 + 240 + 260 + 160 + 150
= 1180
Note: The cells, which are getting allocated is called as basic cells. The number of basic cells in any transportation problem should be equal to (row+column-1). The cells, which are not getting any allocation is known as non-basic cells.
The major advantage of this method is its simplicity to use; however, north-west method does not consider costs, thus, it may lead to more iteration before optimal solution is reached. We will solve the above problem by matrix-minima / least cost method, which gives importance for lowest cost for making allocations.
The procedure for constructing an initial basic feasible solution selects the basic variables one at a time. The North West corner rule, allocation starts to the cell, which occupies the top left-hand corner of the transportation tableau [north-west corner cell / cell- (1, 1)], and proceeds systematically along either a row or a column and make allocations to subsequent cells until the bottom right-hand corner is reached, by which time enough allocations will have been made to constitute an initial solution.
Northwest Corner Method: – Step-by-step procedure
1. Start by selecting the cell in the most \North-West” corner of the table, and set X11 as large as possible (cannot be larger than s1 or d1).
2. Assign the maximum amount to this cell that is allowable based on the requirements and the capacity constraints.
1. If X11 = s1, cross out the first row
[That is exhausting the capacity in the origin].
2. Change d1 to (d1- s1).
[That is modifying the demand after making supply from origin-1 for the market-1].
[That is exhausting the requirements of the market-1].
4. Change s1 to (s1 – d1).
[That is modifying the capacity, after making supply from origin-1 for the market-1].
3. If for any cell, supply equals demand, then the next allocation can be made in cell either in the next row or column; but don’t cross out both the row as well as column. At the row or column, keep a remaining value as zero and make the allocation later to a cell; this will eliminate the process of making dummy basic cells; this issue is called as degeneracy at the initial cell. Degeneracy is reduction in availability of basic cell from the level of (m+n-1).
4. Continue applying procedure to the north-west cell that does not lie in the crossed out row or column until there is one cell left.
We will solve the problem formulated for Adani Power Limited.
Consider the following transportation table.
The north-west corner is cell-(1, 1); the city requirement is 45 and plant-1can supply at most 35.

So we decide the supply the entire 35 to city-1;
Now, the plant-1 cannot supply anymore to any cities; and the demand for city-1 will be reduced to 10, after a supply is allocated from plant-1.
This is given in the following table.

After removing the row-1, again we try to find the north-west corner; this time, it is the cell-(2, 1); the city requirement is 10 and plant-2 can supply at most 50. So we decided to supply the entire requirement of the city-1 [10 units]; now the city-1 requirement is completely fulfilled and removed from further considerations.

And the availability at plant-2 is reduced to 20 units, after making supply to city-2.
This is given in the following table.

So we decided to supply the entire availability at plant-2 [20 units] to the city-3; now the city-2 requirement is reduced to 10 units; however plant-2 is completely exhausted its capacity and hence removed from further considerations.
And the requirement city-3 is reduced to 10 units. This is given in the following table.


X11 = 35; X21= 10; X22= 20; X23= 20 X33= 10; X34= 30 Total transportation cost through the north-west corner method
TC = (35 X 8) + (10 X 9) + (20 X 12) + (20 X 13) + (10 X 16) + (30 X 5)
= 280 + 90 + 240 + 260 + 160 + 150
= 1180
Note: The cells, which are getting allocated is called as basic cells. The number of basic cells in any transportation problem should be equal to (row+column-1). The cells, which are not getting any allocation is known as non-basic cells.
Advantages and disadvantages of North-west corner Method
The major advantage of this method is its simplicity to use; however, north-west method does not consider costs, thus, it may lead to more iteration before optimal solution is reached. We will solve the above problem by matrix-minima / least cost method, which gives importance for lowest cost for making allocations.
Tags : Operations Management - Transportation / Assignment & Inventory Management
Last 30 days 3154 views












