Operations Management - Transportation / Assignment & Inventory Management
Hungarian Algorithm - Assignment Problems
Posted On :
The Hungarian Algorithm is applicable only for minimization models.
Hungarian Algorithm
The Hungarian Algorithm is applicable only for minimization models. In case the problem is not in minimization form, convert the
1. Identify the largest number in the entire matrix / table.
2. Subtract all the entries from the highest number and write down the new reduced table.
3. This
reduced table is in the form of ‘opportunity cost’ of not allocating a resource
to a task; thus, the aim of the problem, which is in the new-reduced format,
after subtracting all the entries from the highest, can be viewed as a
minimization model.
4. Then the
Hungarian method is applied, which is given in the following steps. If the
given problem is a minimization model, you can skip this initiation process.
Also, on occasion, the number of assignees to be assigned to perform tasks will not be equal; that is, the number of rows will not equal to the number of columns. This kind of assignment models are known as unbalanced assignment problems. To apply the Hungarian Algorithm, you have to convert the problem into a balanced assignment problem.
An Assignment problem is known as balanced one, if the number of rows equals to the number of columns. In case, if the given problem is unbalanced one, you have to add appropriate number of rows or columns with zero as assignment cost [dummy row or dummy column] and make the problem as balanced assignment model.
Then the Hungarian method is applied to this modified table, which is given in the following steps. If the given problem is a balanced model, you can skip this initiation process.
Step-1
Subtract the smallest number in each row from every number in the row; this is known as row reduction. Enter the results in a new table.
Step-2
Subtract the smallest number in each column of the new table obtained in Step-1 from every number in the respective column; this is known as column reduction. Enter the results in the new table.
Step-3
Check whether an optimal set of assignments can be made. This is done in the following procedure;
1. Draw minimum number of straight lines to cover all the zeros in the table obtained after column reduction.
2. Straight
lines can be drawn horizontally or vertically but not diagonally.
3. Choose the
row or column that contains the maximum number of zeros and draw the first
line; in case of tie breaker, break it arbitrarily.
4. In the rest of columns / row, find a row or column that contains maximum number of zeros and draw the next line [in case a zero is already covered by a straight line, do not count while drawing the new line].
5. Repeat
the above steps till all the zeros are covered by straight lines.
6. If the minimum of number of straight lines equal to number of rows, an optimal set of assignment is possible; otherwise, go to the Step-4.
Step-4
If the number of straight lines is not equal to the number of rows, then do the following operations in the table, which is just now covered by straight lines.
1. Subtract the smallest uncovered number [not covered by any straight lines] from every uncovered number in the table.
2. Add this
smallest uncovered number to the numbers at intersections of covering lines.
3. Do not
make any changes for those numbers which are covered by straight lines but not
crossed out by lines.
4. Repeat
the step -3 and check the optimal number of allocations; if not repeat the
step-4 again till you gets optimal number of straight lines.
Step-5
If the number of straight lines is equal to the number of rows / columns, then it is an indication of optimum solution can be arrived by using the zero elements.
1. Make the assignments one at a time in positions that have zero elements.
2. Search
with rows or columns that have unique zero; since each row (resource) and
column (task) needs to receive exactly one assignment, you may strike out the
row and the column involved after making the assignment.
3. Then move
on to the other rows and columns that are not crossed out; continue until every
row and every column has exactly one assignment.
This procedure will provide the complete set of assignments and an optimum solution for the problem.
Example-1
Find the assignment of operator to appropriate job with lowest possible time to complete the jobs.
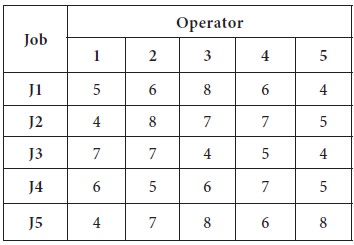
Since the given problem is a minimization model and balanced one, we apply the Hungarian algorithm straight away on the given table.
Step-1
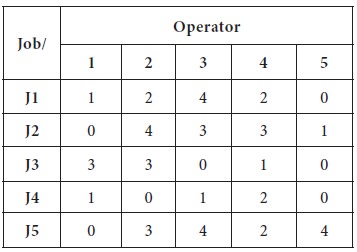
Step-2
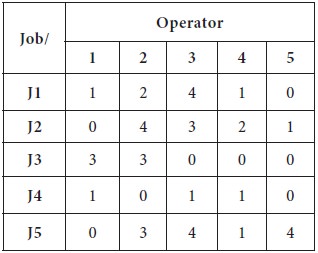
Step-3
Check whether an optimal set of assignments can be made. Draw minimal number straight lines to cover all the zeros.
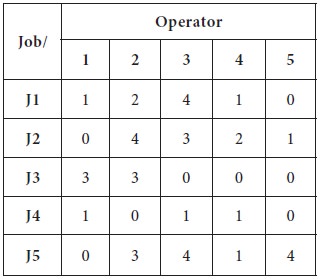
1. The maximum number of zeros is found in row-3 and column-5 [Three zeros each]; the first line is drawn arbitrarily at row-3
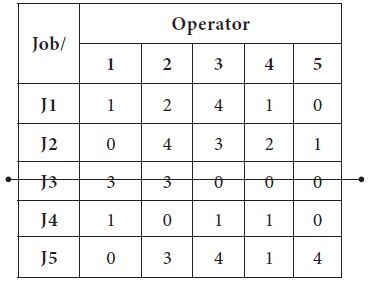
2. In the
new matrix, after drawing the line, maximum number of zeros is found in row-4,
column-1 and column-5 [Two zeros each]; thus the tie is broken arbitrarily and
the second line is drawn at column-5.
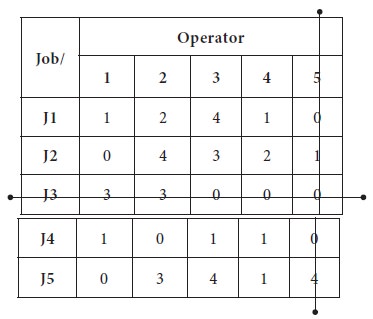
3. In the
new matrix, after drawing the lines, maximum number of zeros is found in,
column-1 [Two zeros each]; thus the tie third line is drawn at column-1.
4. In the
new matrix, after drawing the lines, maximum number of zeros is found in,
column-2 / row-4 [one zero, which is same]; thus the fourth line is drawn at
column-2 arbitrarily.
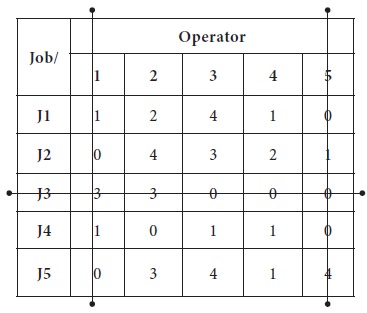
Now the maximum number straight lines needs to
cover all the zeros are four, which is less than the number of rows in the
table. Thus, it is an indication of optimum number of zeros is not there in the
table to make allocation.
Step-4
Since the number of straight lines is not equal to the number of rows, then we do the following operations in the table, which is just now covered by straight lines.
1. Subtract the smallest uncovered number [not covered by any straight lines] from every uncovered number in the table; in the above table, the smallest uncovered number is one.
2. We have
to add one to the numbers at intersections of covering lines; and should not
make any changes for those numbers which are covered by straight lines but not
crossed out by lines.
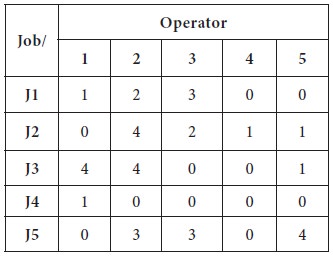
Now in the new matrix, which is obtained above, we
repeat the same process described in the Step-3 to draw straight lines.
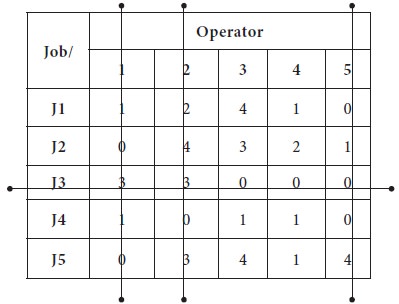
The first line is drawn at Row-4, which is having 4 zeros; then the second line is drawn at Column-4, which is having 3 zeros; the third line is drawn at column-1, which is having 2 zeros; the next line is drawn at row-3 and the last line is drawn at column-5
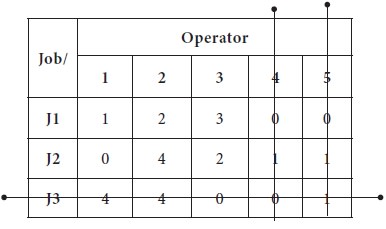
Now the minimum number of straight lines needs to
cover all zeros is equal to the number of rows/ columns, it is an indication of
optimum number of allocation can be made with available zeros.
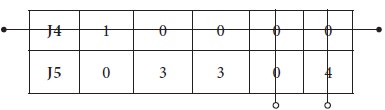
Step-5
We now proceed to make optimum allocation with available zero entries; in the new matrix, jot down all the zeros in their respective positions.
1. Search row wise for a unique zero; if one such zero is found mark it and strike the respective column [zeros]
2. Repeat
the above step; in case unique zero is not available, repeat the above search
column wise; search column wise unique zero and if one such zero is found mark
it and strike the respective row [zeros]
3. Repeat
the above step, until all the zeros are marked. In case of tie breaker, break
the tie arbitrarily.
The first unique zero is found in Row-2 and it is marked; then the column-1 is strike out; the next unique zero is found in row-5 and the same process is repeated. Third unique zero was found again in the row search at row-1; fourth unique zero was found at row-3 and finally the last unique zero was found in row-4.
Now this is an indication of optimum allocation has been made. The respective zero allocation positions are considered as optimum allocation for the given problem.
The Hungarian Algorithm is applicable only for minimization models. In case the problem is not in minimization form, convert the
1. Identify the largest number in the entire matrix / table.
2. Subtract all the entries from the highest number and write down the new reduced table.
Also, on occasion, the number of assignees to be assigned to perform tasks will not be equal; that is, the number of rows will not equal to the number of columns. This kind of assignment models are known as unbalanced assignment problems. To apply the Hungarian Algorithm, you have to convert the problem into a balanced assignment problem.
An Assignment problem is known as balanced one, if the number of rows equals to the number of columns. In case, if the given problem is unbalanced one, you have to add appropriate number of rows or columns with zero as assignment cost [dummy row or dummy column] and make the problem as balanced assignment model.
Then the Hungarian method is applied to this modified table, which is given in the following steps. If the given problem is a balanced model, you can skip this initiation process.
Step-1
Subtract the smallest number in each row from every number in the row; this is known as row reduction. Enter the results in a new table.
Step-2
Subtract the smallest number in each column of the new table obtained in Step-1 from every number in the respective column; this is known as column reduction. Enter the results in the new table.
Step-3
Check whether an optimal set of assignments can be made. This is done in the following procedure;
1. Draw minimum number of straight lines to cover all the zeros in the table obtained after column reduction.
4. In the rest of columns / row, find a row or column that contains maximum number of zeros and draw the next line [in case a zero is already covered by a straight line, do not count while drawing the new line].
6. If the minimum of number of straight lines equal to number of rows, an optimal set of assignment is possible; otherwise, go to the Step-4.
Step-4
If the number of straight lines is not equal to the number of rows, then do the following operations in the table, which is just now covered by straight lines.
1. Subtract the smallest uncovered number [not covered by any straight lines] from every uncovered number in the table.
Step-5
If the number of straight lines is equal to the number of rows / columns, then it is an indication of optimum solution can be arrived by using the zero elements.
1. Make the assignments one at a time in positions that have zero elements.
This procedure will provide the complete set of assignments and an optimum solution for the problem.
Example-1
Find the assignment of operator to appropriate job with lowest possible time to complete the jobs.

Since the given problem is a minimization model and balanced one, we apply the Hungarian algorithm straight away on the given table.
Step-1
Subtract the minimum value
in each row from all other respective row values:

Step-2
Subtract the minimum value
in each column from all other respective column values:

Step-3
Check whether an optimal set of assignments can be made. Draw minimal number straight lines to cover all the zeros.

1. The maximum number of zeros is found in row-3 and column-5 [Three zeros each]; the first line is drawn arbitrarily at row-3




Since the number of straight lines is not equal to the number of rows, then we do the following operations in the table, which is just now covered by straight lines.
1. Subtract the smallest uncovered number [not covered by any straight lines] from every uncovered number in the table; in the above table, the smallest uncovered number is one.

The first line is drawn at Row-4, which is having 4 zeros; then the second line is drawn at Column-4, which is having 3 zeros; the third line is drawn at column-1, which is having 2 zeros; the next line is drawn at row-3 and the last line is drawn at column-5


Step-5
We now proceed to make optimum allocation with available zero entries; in the new matrix, jot down all the zeros in their respective positions.
1. Search row wise for a unique zero; if one such zero is found mark it and strike the respective column [zeros]
The first unique zero is found in Row-2 and it is marked; then the column-1 is strike out; the next unique zero is found in row-5 and the same process is repeated. Third unique zero was found again in the row search at row-1; fourth unique zero was found at row-3 and finally the last unique zero was found in row-4.
Now this is an indication of optimum allocation has been made. The respective zero allocation positions are considered as optimum allocation for the given problem.

Tags : Operations Management - Transportation / Assignment & Inventory Management
Last 30 days 1034 views












