Home | ARTS | Operations Management
|
Variations in Assignment Problem- Case 2: Unbalanced Models - Assignment Problems
Operations Management - Transportation / Assignment & Inventory Management
Variations in Assignment Problem- Case 2: Unbalanced Models - Assignment Problems
Posted On :
In case, if the given problem is unbalanced one, you have to add appropriate number of rows or columns with zero as assignment cost [dummy row or dummy column] and make the problem as balanced assignment model.
Variations in Assignment
Problem- Case 2: Unbalanced Models
1. An Assignment problem is known as balanced one, if the number of rows equals to the number of columns.
2. When the number of rows is not equal to number of
columns, the assignment models are called as unbalanced assignment problems.
3. In case, if the given problem is unbalanced one, you have to add appropriate number of rows or columns with zero as assignment cost [dummy row or dummy column] and make the problem as balanced assignment model.
Exercise-1
A university wants to allocate the four subjects and six teachers claim that they have the required competencies!! /knowledge!! to teach all the subjects. The dean believes that the failure in the course is reflection of faculty member’s performance! Allocate the subject to appropriate
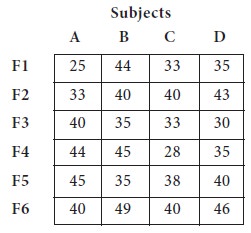
Solution
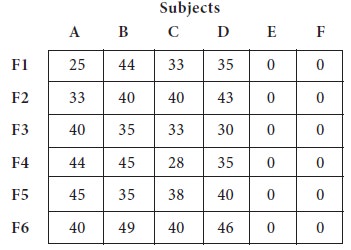
You may notice that the number of rows (6) not equal to the number of columns (4); thus, the given problem is an example of unbalanced assignment models. We add two dummy columns (2 dummy subjects) with zero as number failures. The modified problem becomes a balanced one and the initial table is given below;
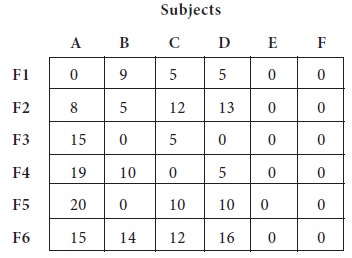
Now we can use Hungarian algorithm, which requires
a balanced one to apply. The following table is obtained after column
reduction, since row reduction will give the same table above.
1. The first
straight line is drawn at Column-5 and second is at Column-6, which are having
six zeros each.
2. The next
line is drawn at Row-3
3. Fourth line is drawn at Row-1; fifth at Row-4; the last line at Row-5
4. Since the number of straight lines equal to number of rows/columns,
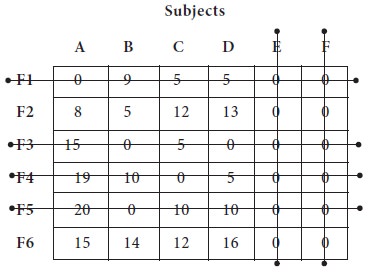
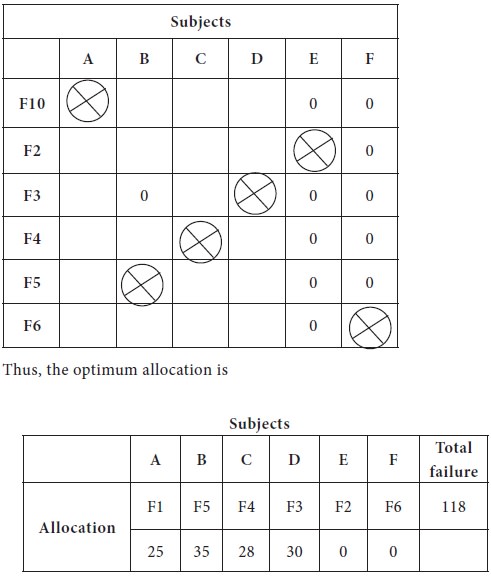
The next step is to consider the zeros and making the allocations. Since, every row is having zeros; we do the column wise search;
1. Column-1,
Column-3 & Column-4 are having unique zero, we mark them for allocation and
cross out the respective rows in which the zero appear.
2. In the
process, we get unique zero in Column-2 and strike out the Row-5
3. Now we
have tie at Row-2 and Row-6, which can be broken arbitrarily.
4. We
allocate Row-2 to Column 5 (E) and Row-6 to Column-6 (F).
1. An Assignment problem is known as balanced one, if the number of rows equals to the number of columns.
3. In case, if the given problem is unbalanced one, you have to add appropriate number of rows or columns with zero as assignment cost [dummy row or dummy column] and make the problem as balanced assignment model.
Exercise-1
A university wants to allocate the four subjects and six teachers claim that they have the required competencies!! /knowledge!! to teach all the subjects. The dean believes that the failure in the course is reflection of faculty member’s performance! Allocate the subject to appropriate

You may notice that the number of rows (6) not equal to the number of columns (4); thus, the given problem is an example of unbalanced assignment models. We add two dummy columns (2 dummy subjects) with zero as number failures. The modified problem becomes a balanced one and the initial table is given below;


3. Fourth line is drawn at Row-1; fifth at Row-4; the last line at Row-5
4. Since the number of straight lines equal to number of rows/columns,

The next step is to consider the zeros and making the allocations. Since, every row is having zeros; we do the column wise search;

Tags : Operations Management - Transportation / Assignment & Inventory Management
Last 30 days 3635 views












