Research Methodology - Statistical Analysis
POISSON DISTRIBUTION - Statistical Analysis
Posted On :
Poisson distribution was derived in 1837 by a French Mathematician Simeon D Poisson (1731 – 1840).
POISSON DISTRIBUTION
Poisson distribution was derived in 1837 by a French Mathematician Simeon D Poisson (1731 – 1840). In binomial distribution, the values of p and q and n are given. There is a certainty of the total number of events. But there are cases where p is very small and n is very large and such case is normally related to poisson distribution. For example, persons killed in road accidents, the number of defective articles produced by a quality machine. Poisson distribution may be obtained as a limiting case of binomial probability distribution, under the following condition.
i. P, successes, approach zero (p 0)
0)
ii. np = m is finite.
The poisson distribution of the probabilities of occurrence of various rare events (successes) 0,1,2,…. Are given below:

Where, e = 2.718, and m = average number of occurrence of given distribution.
The poisson distribution is a discrete distribution with a parameter m.
The various constants are:

Illustration:
A book contains 100 misprints distributed randomly throughout its 100 pages. What is the probability that a page observed at random contains at least two misprints? Assume Poisson Distribution.

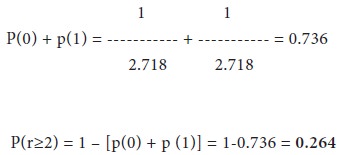
Illustration:
If the mean of a Poisson distribution is 16, find (1) S.D.(2) B1 (3) B2 (4) µ3 (5) µ4
Poisson distribution was derived in 1837 by a French Mathematician Simeon D Poisson (1731 – 1840). In binomial distribution, the values of p and q and n are given. There is a certainty of the total number of events. But there are cases where p is very small and n is very large and such case is normally related to poisson distribution. For example, persons killed in road accidents, the number of defective articles produced by a quality machine. Poisson distribution may be obtained as a limiting case of binomial probability distribution, under the following condition.
i. P, successes, approach zero (p
ii. np = m is finite.
The poisson distribution of the probabilities of occurrence of various rare events (successes) 0,1,2,…. Are given below:

Where, e = 2.718, and m = average number of occurrence of given distribution.
The poisson distribution is a discrete distribution with a parameter m.
The various constants are:

Illustration:
A book contains 100 misprints distributed randomly throughout its 100 pages. What is the probability that a page observed at random contains at least two misprints? Assume Poisson Distribution.

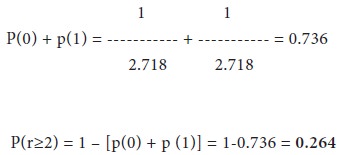
Illustration:
If the mean of a Poisson distribution is 16, find (1) S.D.(2) B1 (3) B2 (4) µ3 (5) µ4
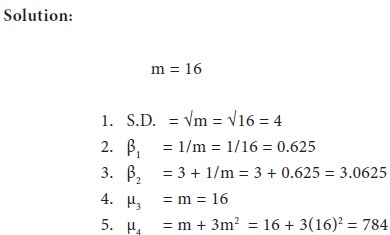
Tags : Research Methodology - Statistical Analysis
Last 30 days 791 views












