Operations Management - Introduction to Operations Research
Duality – Introduction
Posted On :
The term dual in the general sense means implies two or double. In the context of linear programming duality implies that each programming problem can be analyzed in two different ways but having equivalent solutions.
Duality – Introduction
The term dual in the general sense means implies two or double. In the context of linear programming duality implies that each programming problem can be analyzed in two different ways but having equivalent solutions. Associated with every linear programming problem whether it is maximization or minimization type there exist another linear programming problem, which is based upon same data, and having same solution. The original problem is called the primal problem while the associated one is called its dual problem.
The concept of duality is based on the fact that any linear programming must be first put in its standard form before solving the problem by simplex method. Since all the primal-dual computations are
The format of the Simplex method is such that solving one type of problem is equivalent to solving the other simultaneously.
Thus, if the optimal solution to one is known, then optimal solution of the other can also be read from the final simplex table.
In some cases, considerable computing time can be saved by solving the dual.
The importance of the duality concept is due to two main reasons.
1. Firstly, if the primal contains a large number of constraints and a smaller number of variables, converting it to the dual problem and then solving it can considerably reduce the labor of computation.
2. Secondly, the interpretation of the dual variables from the cost or economic point of view proves extremely useful in making future decisions in the activities being programmed.
Various steps involved in formulation of a primal-dual pair are:
Step 1
Put the given linear programming problem into its standard form. Consider it as a primal problem.
Step 2
Identify the variables to be used in the dual problem. For each constraint, assign one dual variable. The number of the variables in the dual problem will be equal to the number of constraint equations in the primal problem.
Step 3
1. Write down the objective function of the dual, using the right hand side constants of the primal constraints.
2. If the problem is of maximization type, the dual will be a minimization problem and vice versa.
Step 4
Make use of dual variable identified in Step 2; write down the constraints for the dual problem.
a. If the primal is a maximization problem, the dual constraints must be all of ‘>=’ type and vice versa.
b. The column coefficients of the primal constraints become the row coefficients of the dual constraints.
c. The coefficients of the primal objective function become the right hand side constants of the dual constraints.
d. The dual variables are defined to be unrestricted in sign.
Step 5
Using steps 3 and 4, write down the dual of the L. P. P
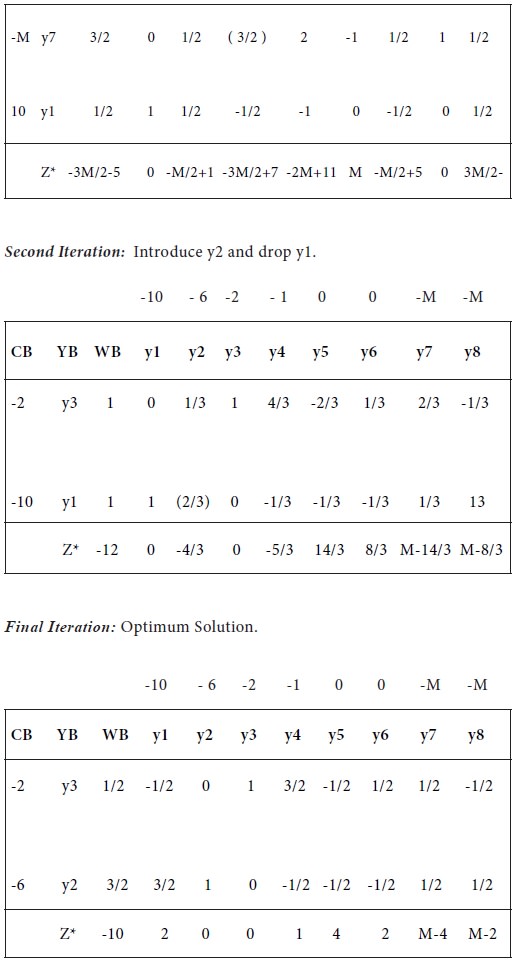
Thus an optimum feasible solution to the dual problem is
w1=0, w2=3/2, w3=1/2;
Min Z*= - (- 10) =10
The term dual in the general sense means implies two or double. In the context of linear programming duality implies that each programming problem can be analyzed in two different ways but having equivalent solutions. Associated with every linear programming problem whether it is maximization or minimization type there exist another linear programming problem, which is based upon same data, and having same solution. The original problem is called the primal problem while the associated one is called its dual problem.
The concept of duality is based on the fact that any linear programming must be first put in its standard form before solving the problem by simplex method. Since all the primal-dual computations are
The format of the Simplex method is such that solving one type of problem is equivalent to solving the other simultaneously.
Thus, if the optimal solution to one is known, then optimal solution of the other can also be read from the final simplex table.
In some cases, considerable computing time can be saved by solving the dual.
The importance of the duality concept is due to two main reasons.
1. Firstly, if the primal contains a large number of constraints and a smaller number of variables, converting it to the dual problem and then solving it can considerably reduce the labor of computation.
2. Secondly, the interpretation of the dual variables from the cost or economic point of view proves extremely useful in making future decisions in the activities being programmed.
Steps In Formulating The Dual Problem
Various steps involved in formulation of a primal-dual pair are:
Step 1
Put the given linear programming problem into its standard form. Consider it as a primal problem.
Step 2
Identify the variables to be used in the dual problem. For each constraint, assign one dual variable. The number of the variables in the dual problem will be equal to the number of constraint equations in the primal problem.
1. Write down the objective function of the dual, using the right hand side constants of the primal constraints.
2. If the problem is of maximization type, the dual will be a minimization problem and vice versa.
Step 4
Make use of dual variable identified in Step 2; write down the constraints for the dual problem.
a. If the primal is a maximization problem, the dual constraints must be all of ‘>=’ type and vice versa.
b. The column coefficients of the primal constraints become the row coefficients of the dual constraints.
c. The coefficients of the primal objective function become the right hand side constants of the dual constraints.
d. The dual variables are defined to be unrestricted in sign.
Step 5
Using steps 3 and 4, write down the dual of the L. P. P
Advantages of duality
1. It is advantageous to solve the dual of a primal having fewer constraints, because the number of constraints usually equals the number of iteration required to solve the problem.
2. It also avoids the necessary for adding surplus or artificial variables and solves the problem quickly (i.e. primal-dual algorithm). In economics, duality is useful in the formulation of the input and output systems.
3. The dual variables provide n important economic interpretation of the final solution of an LP problem.
4. It is quite useful when investigating changes in the coefficients or formulation of an LP problem (i.e. in sensitivity analysis).
5. Duality is used to solve an LP problem by the Simplex method in which the initial solution is infeasible (i.e. the dual simplex method).
1. It is advantageous to solve the dual of a primal having fewer constraints, because the number of constraints usually equals the number of iteration required to solve the problem.
2. It also avoids the necessary for adding surplus or artificial variables and solves the problem quickly (i.e. primal-dual algorithm). In economics, duality is useful in the formulation of the input and output systems.
3. The dual variables provide n important economic interpretation of the final solution of an LP problem.
4. It is quite useful when investigating changes in the coefficients or formulation of an LP problem (i.e. in sensitivity analysis).
5. Duality is used to solve an LP problem by the Simplex method in which the initial solution is infeasible (i.e. the dual simplex method).
Example-1
Write the dual of the following linear programming problem:
Maximize Z=x1-x2+3x3
Subject to the constraints:
x1+x2+x3<=10
2x1-0x2-x3<=2
2x1-2x2-3x3<=6
Where x1, x2, x3>=0
Solution
If W1, W2, W3 be the dual variable corresponding to the primal constraints.
Then, the dual problem will be
Minimize Z=10W1+2W2+6W3
Subject to the constraints:
W1+2W2+2W3>=1
W1-2W3>=-1
W1-W2-3W3>=3
Where W1, W2, W3 >=0
Example-2
Max Z=3x1+10x2+2x3
Subject to
2x1+3x2+2x3<=7
3x1-2x2+4x3=3
And x1, x2, x3 >=0
Solution
Given the primal LPP is
Max Z=3x1+10 x2+2x3
Subject to
2x1+3x2+2x3<=7
3x1-2x2+4x3=3
And x1, x2, x3 >=0
Since the primal problem contains 2 constraints and 3 variables, the dual problem will contain 3 constraints and 2 dual variables Y1, Y2.
Also, since the second constraint in the primal problem is with equality, the corresponding second dual variable Y2 is unrestricted in sign.
Therefore, the dual problem is
Min W=7Y1+3Y2
Subject to
2Y1+3Y2>=3
3Y1-2Y2>=10
2Y1+4Y2>=2
And Y1>=0, & Y2 is unrestricted.
Important theorems’ statement used in Primal -Dual context
1. The dual of the dual is primal.
2. If either the primal or the dual problem has an unbound objective function value, then the other problem has no feasible solution is known as Existence theorem.
3. If the primal or the dual has a finite optimum solution, then the other problem also possess a finite optimum solution and the optimum
values of the objective functions of the two problems are equal is called Fundamental theorem of duality.
4. Each basic feasible solution in primal problem is related to a complementary basic feasible solution in dual problem.
5. Complementary slackness theorem:
a) If a primal variable is positive, then the corresponding dual constraint is an equation at the optimum and vice versa.
b) If a primal constraint is a strict inequality, then the corresponding
6. If dual has no feasible solution, then primal also admits no feasible solution.
If primal is a maximization problem, then following are the set of rules that govern the derivation of the optimum solution:
Rule 1
Corresponding net evaluations of the starting primal variables=Difference between the left and right sides of the dual constraints associated with the starting primal variables.
Rule 2
Negative of the corresponding net evaluations of the starting dual variables equal to the difference between the left and right sides of the primal constraints associated with the starting dual variables.
Rule 3
If the primal (dual) problem is unbounded, then the dual (primal) problem does not have any feasible solution.
Example-1
Use duality to solve the following L.P.P:
Maximize Z=2X1+X2
Subject to constraints:
X1+2X2<=10
X1+X2<=6
X1-X2<=2
X1-2X2<=1
X1, X2, X3>=0
Solution
The dual problem of the given primal is
Minimize Z*=10Y1+6Y2+2Y3+Y4
Subject to constraints:
Y1+Y2+Y3+Y4>=2
2Y1+Y2-Y3-2Y4>=1
Y1, Y2, Y3, Y4>=0
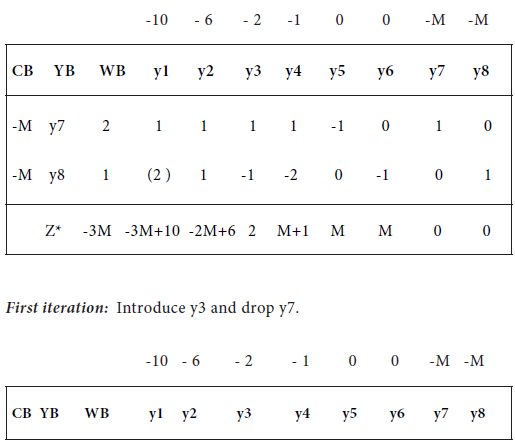
Introducing surplus variables s1>=0, s2>=0 and artificial variables A1>=0, A2>=0, an initial basic feasible solution is A1=2 and A2=1.
The iterative simplex tables are:
Introduce y1 and drop y8.
Write the dual of the following linear programming problem:
Maximize Z=x1-x2+3x3
Subject to the constraints:
x1+x2+x3<=10
2x1-0x2-x3<=2
2x1-2x2-3x3<=6
Where x1, x2, x3>=0
Solution
If W1, W2, W3 be the dual variable corresponding to the primal constraints.
Then, the dual problem will be
Minimize Z=10W1+2W2+6W3
Subject to the constraints:
W1+2W2+2W3>=1
W1-2W3>=-1
W1-W2-3W3>=3
Where W1, W2, W3 >=0
Example-2
Max Z=3x1+10x2+2x3
Subject to
2x1+3x2+2x3<=7
3x1-2x2+4x3=3
And x1, x2, x3 >=0
Solution
Given the primal LPP is
Max Z=3x1+10 x2+2x3
Subject to
3x1-2x2+4x3=3
And x1, x2, x3 >=0
Since the primal problem contains 2 constraints and 3 variables, the dual problem will contain 3 constraints and 2 dual variables Y1, Y2.
Also, since the second constraint in the primal problem is with equality, the corresponding second dual variable Y2 is unrestricted in sign.
Therefore, the dual problem is
Min W=7Y1+3Y2
Subject to
2Y1+3Y2>=3
3Y1-2Y2>=10
2Y1+4Y2>=2
And Y1>=0, & Y2 is unrestricted.
Important theorems’ statement used in Primal -Dual context
1. The dual of the dual is primal.
2. If either the primal or the dual problem has an unbound objective function value, then the other problem has no feasible solution is known as Existence theorem.
3. If the primal or the dual has a finite optimum solution, then the other problem also possess a finite optimum solution and the optimum
values of the objective functions of the two problems are equal is called Fundamental theorem of duality.
4. Each basic feasible solution in primal problem is related to a complementary basic feasible solution in dual problem.
5. Complementary slackness theorem:
a) If a primal variable is positive, then the corresponding dual constraint is an equation at the optimum and vice versa.
b) If a primal constraint is a strict inequality, then the corresponding
6. If dual has no feasible solution, then primal also admits no feasible solution.
Duality and Simplex Method
If primal is a maximization problem, then following are the set of rules that govern the derivation of the optimum solution:
Rule 1
Corresponding net evaluations of the starting primal variables=Difference between the left and right sides of the dual constraints associated with the starting primal variables.
Rule 2
Negative of the corresponding net evaluations of the starting dual variables equal to the difference between the left and right sides of the primal constraints associated with the starting dual variables.
Rule 3
If the primal (dual) problem is unbounded, then the dual (primal) problem does not have any feasible solution.
Example-1
Use duality to solve the following L.P.P:
Maximize Z=2X1+X2
Subject to constraints:
X1+2X2<=10
X1+X2<=6
X1-X2<=2
X1-2X2<=1
X1, X2, X3>=0
Solution
The dual problem of the given primal is
Minimize Z*=10Y1+6Y2+2Y3+Y4
Subject to constraints:
Y1+Y2+Y3+Y4>=2
2Y1+Y2-Y3-2Y4>=1
Y1, Y2, Y3, Y4>=0
Introducing surplus variables s1>=0, s2>=0 and artificial variables A1>=0, A2>=0, an initial basic feasible solution is A1=2 and A2=1.
The iterative simplex tables are:
Initial Iteration
Introduce y1 and drop y8.


Thus an optimum feasible solution to the dual problem is
w1=0, w2=3/2, w3=1/2;
Min Z*= - (- 10) =10
Tags : Operations Management - Introduction to Operations Research
Last 30 days 2782 views












