Operations Management - Network Problems
Solution For The Example Problem - Shortest Path Problem
Posted On :
Looking at the diagram, we see that node 1 is the origin and the nodes 2 and 3 are neighbours to the origin. Among the two nodes, we see that node 2 is at a distance of 40 units from node 1 whereas node 3 is at a distance of 100 units from node 1. The minimum of {40, 100} is 40.
Solution For The Example
Problem
Looking at the diagram, we see that node 1 is the origin and the nodes 2 and 3 are neighbours to the origin. Among the two nodes, we see that node 2 is at a distance of 40 units from node 1 whereas node 3 is at a distance of 100 units from node 1. The minimum of {40, 100} is 40. Thus, the node nearest to the origin is node 2, with a distance of 40 units. So, out of the two nodes 2 and 3, we select node 2. We form a set of nodes {1, 2} and construct a path connecting the node 2 with node 1 by a thick line and mark the distance of 40 in a box by the side of node 2. This first iteration is shown in the following diagram.
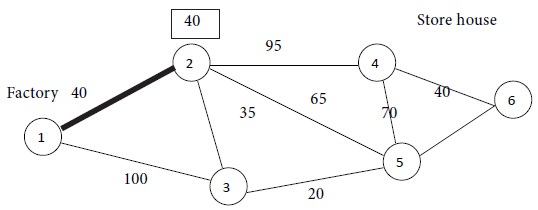
Now we search for the next node nearest to the set of nodes {1, 2}. For this purpose, consider those nodes which are neighbours of either node 1 or node 2. The nodes 3, 4 and 5 fulfill this condition. We calculate the following distances.
The distance between nodes 1 and 3 = 100.
The distance between nodes 2 and 3 = 35.
The distance between nodes 2 and 4 = 95.
The distance between nodes 2 and 5 = 65.
Minimum of {100, 35, 95, 65} = 35.
Therefore, node 3 is the nearest one to the set {1, 2}. In view of this observation, the set of nodes is enlarged from {1, 2} to {1, 2, 3}. For the set {1, 2, 3}, there are two possible paths, viz. Path 1 → 2 → 3 and Path 1 → 3 →2. The Path 1 → 2 → 3 has a distance of 40 + 35 = 75 units while the Path 1 → 3 → 2 has a distance of 100 + 35 = 135 units.
Minimum of {75, 135} = 75. Hence we select the path 1 → 2 → 3 and display this path by thick edges. The distance 75 is marked in a box by the side of node 3. We obtain the following diagram at the end of Iteration No. 2.
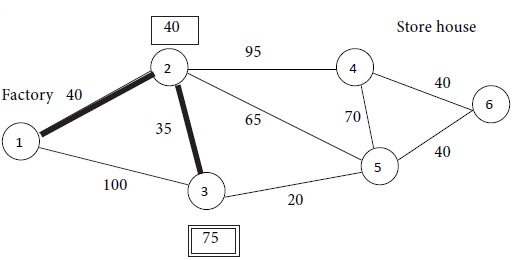
Iteration No. 2
We repeat the process. The next node nearest to the set {1, 2, 3} is either node 4 or node 5.
Node 4 is at a distance of 95 units from node 2 while node 2 is at a distance of 40 units from node 1. Thus, node 4 is at a distance of 95 + 40 = 135 units from the origin.
As regards node 5, there are two paths viz. 2 → 5 and 3 → 5, providing a link to the origin. We already know the shortest routes from nodes 2 and 3 to the origin. The minimum distances have been indicated in boxes near these nodes. The path 3 → 5 involves the shortest distance. Thus, the distance between nodes 1 and 5 is 95 units (20 units between nodes 5 and 3 + 75 units between node 3 and the origin). Therefore, we select node 5 and enlarge the set from {1, 2, 3} to {1, 2, 3, 5}. The distance 95 is marked in a box by the side of node 5. The following diagram is obtained at the end of Iteration No. 3.
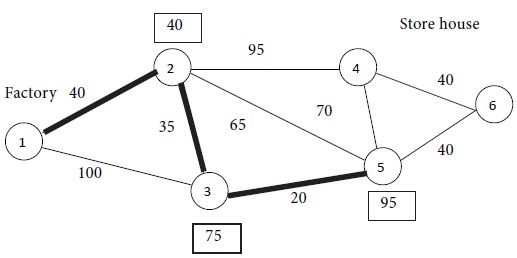
Now 2 nodes remain, viz., nodes 4 and 6. Among them, node 4 is at a distance of 135 units from the origin (95 units from node 4 to node 2 + 40 units from node 2 to the origin). Node 6 is at a distance of 135 units from the origin (40 + 95 units). Therefore, nodes 4 and 6 are at equal distances from the origin. If we choose node 4, then travelling from node 4
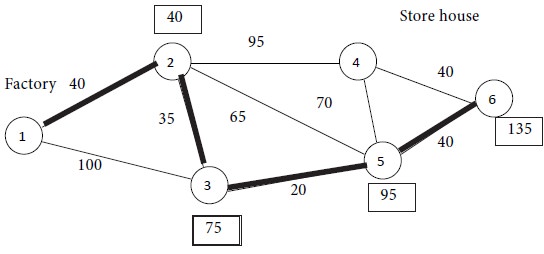
Iteration No. 4
Referring to the above diagram, we see that the
shortest route is provided by the path 1 → 2 → 3 → 5 → 6 with a minimum
distance of 135 units.
Looking at the diagram, we see that node 1 is the origin and the nodes 2 and 3 are neighbours to the origin. Among the two nodes, we see that node 2 is at a distance of 40 units from node 1 whereas node 3 is at a distance of 100 units from node 1. The minimum of {40, 100} is 40. Thus, the node nearest to the origin is node 2, with a distance of 40 units. So, out of the two nodes 2 and 3, we select node 2. We form a set of nodes {1, 2} and construct a path connecting the node 2 with node 1 by a thick line and mark the distance of 40 in a box by the side of node 2. This first iteration is shown in the following diagram.

Iteration No. 1
Now we search for the next node nearest to the set of nodes {1, 2}. For this purpose, consider those nodes which are neighbours of either node 1 or node 2. The nodes 3, 4 and 5 fulfill this condition. We calculate the following distances.
The distance between nodes 1 and 3 = 100.
The distance between nodes 2 and 3 = 35.
The distance between nodes 2 and 4 = 95.
The distance between nodes 2 and 5 = 65.
Minimum of {100, 35, 95, 65} = 35.
Therefore, node 3 is the nearest one to the set {1, 2}. In view of this observation, the set of nodes is enlarged from {1, 2} to {1, 2, 3}. For the set {1, 2, 3}, there are two possible paths, viz. Path 1 → 2 → 3 and Path 1 → 3 →2. The Path 1 → 2 → 3 has a distance of 40 + 35 = 75 units while the Path 1 → 3 → 2 has a distance of 100 + 35 = 135 units.
Minimum of {75, 135} = 75. Hence we select the path 1 → 2 → 3 and display this path by thick edges. The distance 75 is marked in a box by the side of node 3. We obtain the following diagram at the end of Iteration No. 2.

Repeating The Process
We repeat the process. The next node nearest to the set {1, 2, 3} is either node 4 or node 5.
Node 4 is at a distance of 95 units from node 2 while node 2 is at a distance of 40 units from node 1. Thus, node 4 is at a distance of 95 + 40 = 135 units from the origin.
As regards node 5, there are two paths viz. 2 → 5 and 3 → 5, providing a link to the origin. We already know the shortest routes from nodes 2 and 3 to the origin. The minimum distances have been indicated in boxes near these nodes. The path 3 → 5 involves the shortest distance. Thus, the distance between nodes 1 and 5 is 95 units (20 units between nodes 5 and 3 + 75 units between node 3 and the origin). Therefore, we select node 5 and enlarge the set from {1, 2, 3} to {1, 2, 3, 5}. The distance 95 is marked in a box by the side of node 5. The following diagram is obtained at the end of Iteration No. 3.

Iteration No. 3
Now 2 nodes remain, viz., nodes 4 and 6. Among them, node 4 is at a distance of 135 units from the origin (95 units from node 4 to node 2 + 40 units from node 2 to the origin). Node 6 is at a distance of 135 units from the origin (40 + 95 units). Therefore, nodes 4 and 6 are at equal distances from the origin. If we choose node 4, then travelling from node 4

Minimum Distance
Tags : Operations Management - Network Problems
Last 30 days 1119 views












