Home | ARTS | Operations Management
|
Model 2 - Determining Economic Order Quantities-Deterministic Models – Purchase Order Quantities without shortages
Operations Management - Transportation / Assignment & Inventory Management
Model 2 - Determining Economic Order Quantities-Deterministic Models – Purchase Order Quantities without shortages
Posted On :
Determination of the optimum batch quantity [EBQ] if the demand is known and uniform with a finite rate of replenishment
Model 2
Determination of the optimum batch quantity [EBQ] if the demand is known and uniform with a finite rate of replenishment
An Illustration: Consider the example, which is given in the Model
1. Assume that you are requiring Rs. 100 per day and in a month your demand is Rs. 3000/- to manage your requirements. Again, you may get your required amount immediately. Only the change is, instead of giving your demand Rs. 3000/- in a single stroke, your parents decided to give the sum in such a way that first 20 days, you will be given with Rs. 150/-per day out of which Rs. 100/- per day is incurred and every day you have to save Rs. 50/- for the first twenty days, and you will not be given any amount after 20th. The remaining days in the month, you will start using the ‘savings’.
If we consider companies such as Hyundai, Maruti and other bigger automobiles, they use to follow this kind of ‘constant rate of replenishment’ instead of instantaneous replenishment. If a truck manufacturer who is placing an order of 10,000 Tires would appreciate the concept of finite rate of fulfilling the orders rather than getting all the 10,000 Tires in a single stroke. He may save a lot in keeping smaller warehouse(s) capital locked in inventory is minimal. For the supplier also, he finds it convenient to sending the quantities in batches rather than bulk dispatches.

Example-1
Gee. Vee. Bearing Ltd has to supply 10000 bearings per day to a SMS Automobiles Ltd., who is assembling some of the components of an automobile company. Mr. Stephen, who is production in-charge, finds that when he starts a production run, he can produce 25000 bearings per day. The cost of holding a bearing in stock per year is 12 paise and the set up cost of a production run is Rs. 1800/= How frequently should the production run be made, and what is the optimum quantity to be produced.

Example-2
S.G. Computers is assembling 50 personal computers per day. The demand occurs at the rate of 25 per day. If the procurement cost of components costs the firm Rs. 250 per batch and the holding cost of a quality checked and packaged computers in warehouse is Rs. 10 per unit per day. Find the economic batch size for one run, assuming the shortages are not permitted. Find the minimum total cost for one run if the cost of the one personal computer is Rs. 15000.

Example-4
Ram Publications finds that demand for their Operations Research books is 24000 books per year. The book publisher can print 4500 copies of the book in a month. The set up cost per set up is Rs. 350/- The rental for the warehouse is Rs. 700 per month. For the books, he pays Rs. 150 as insurance premium per month. He appointed a Storekeeper who can handle all the transactions as well as physical handling of the books, for which he pays Rs. 1500 as salary. Find the EOQ for the above production schedule.

Example-5
SMS Motor Company, the 2-wheeler manufacturer producing 2,50,000 units of mopeds per annum. The company is having its own tyre-manufacturing unit, which is producing tyres for internal consumption as well as acting as ‘Original Equipment Manufacturer’ for several 2-wheelers manufacturers in India. The tyre-manufacturing unit is in a possession to manufacture 20,000 tyres per day as far as any model is concerned and, will be in a position to produce 8,500 tyres per day as far as internal requirements are concerned. Whenever, the production operations starts on one specific type or model, again to produce a new model we have to re set the equipments which will costs Rs. 2500/ per setting. To hold one tyre in inventory, the company has to incur Rs. 100 per year. Assuming 250 working days per year, what will be the optimum manufacturing quantity?
Determination of the optimum batch quantity [EBQ] if the demand is known and uniform with a finite rate of replenishment
An Illustration: Consider the example, which is given in the Model
1. Assume that you are requiring Rs. 100 per day and in a month your demand is Rs. 3000/- to manage your requirements. Again, you may get your required amount immediately. Only the change is, instead of giving your demand Rs. 3000/- in a single stroke, your parents decided to give the sum in such a way that first 20 days, you will be given with Rs. 150/-per day out of which Rs. 100/- per day is incurred and every day you have to save Rs. 50/- for the first twenty days, and you will not be given any amount after 20th. The remaining days in the month, you will start using the ‘savings’.
If we consider companies such as Hyundai, Maruti and other bigger automobiles, they use to follow this kind of ‘constant rate of replenishment’ instead of instantaneous replenishment. If a truck manufacturer who is placing an order of 10,000 Tires would appreciate the concept of finite rate of fulfilling the orders rather than getting all the 10,000 Tires in a single stroke. He may save a lot in keeping smaller warehouse(s) capital locked in inventory is minimal. For the supplier also, he finds it convenient to sending the quantities in batches rather than bulk dispatches.
Solution
Let us have the following assumptions:
1. Demand is known and uniform
2. Let ‘r’ be the rate of demand per unit of time.
3. Shortages are not permitted.
4. Inventory is replenished at the rate of ‘k’ units per unit of time.
5. Let the supply of the items be instantaneous.
6. Lead-time is zero.
Let us have the following assumptions:
1. Demand is known and uniform
2. Let ‘r’ be the rate of demand per unit of time.
3. Shortages are not permitted.
4. Inventory is replenished at the rate of ‘k’ units per unit of time.
5. Let the supply of the items be instantaneous.
6. Lead-time is zero.
7.
Let Q be
the EBQ for each cycle.
8. Let Cs be the set up cost per cycle.
9. Let C1 be the holding cost per unit, per unit
Let us divide the total time say 1-year into ‘n’ equal parts, each of duration‘t’.
Therefore n * t = 1
8. Let Cs be the set up cost per cycle.
9. Let C1 be the holding cost per unit, per unit
Let us divide the total time say 1-year into ‘n’ equal parts, each of duration‘t’.
Therefore n * t = 1
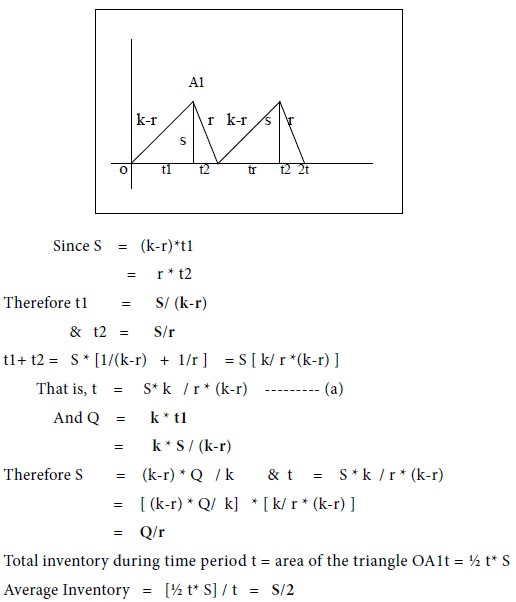
Let us further divide time ‘t’
into 2 parts, say t1 and t2 such that (1) Inventory
is building up at a constant rate of ‘k-r’ units per unit time during t1. (2)
There is no replenishment during time t2 and the inventory is decreasing at the
rate of ‘r’ units per unit time.
At the end of time t1, let S be the level of the inventory and at the end of time t2, zero is the level of inventory. The graph is as follows:
At the end of time t1, let S be the level of the inventory and at the end of time t2, zero is the level of inventory. The graph is as follows:


Example-1
Gee. Vee. Bearing Ltd has to supply 10000 bearings per day to a SMS Automobiles Ltd., who is assembling some of the components of an automobile company. Mr. Stephen, who is production in-charge, finds that when he starts a production run, he can produce 25000 bearings per day. The cost of holding a bearing in stock per year is 12 paise and the set up cost of a production run is Rs. 1800/= How frequently should the production run be made, and what is the optimum quantity to be produced.

Example-2
S.G. Computers is assembling 50 personal computers per day. The demand occurs at the rate of 25 per day. If the procurement cost of components costs the firm Rs. 250 per batch and the holding cost of a quality checked and packaged computers in warehouse is Rs. 10 per unit per day. Find the economic batch size for one run, assuming the shortages are not permitted. Find the minimum total cost for one run if the cost of the one personal computer is Rs. 15000.

Example-3
Shriram Industries, a manufacturer of television cabinets, has to supply his customers 24000 units of television cabinets (shells alone) per year. And, the company can produce the shells at a rate of 3000 per month. The cost of one preparation of the equipments for the production run is Rs. 500/- and the holding cost of one cabinet per month is 15 paisa. Determine the optimum manufacturing quantity, optimum interval between the set ups and total cost, if the cost of one cabinet is Rs. 775/-

Shriram Industries, a manufacturer of television cabinets, has to supply his customers 24000 units of television cabinets (shells alone) per year. And, the company can produce the shells at a rate of 3000 per month. The cost of one preparation of the equipments for the production run is Rs. 500/- and the holding cost of one cabinet per month is 15 paisa. Determine the optimum manufacturing quantity, optimum interval between the set ups and total cost, if the cost of one cabinet is Rs. 775/-

Example-4
Ram Publications finds that demand for their Operations Research books is 24000 books per year. The book publisher can print 4500 copies of the book in a month. The set up cost per set up is Rs. 350/- The rental for the warehouse is Rs. 700 per month. For the books, he pays Rs. 150 as insurance premium per month. He appointed a Storekeeper who can handle all the transactions as well as physical handling of the books, for which he pays Rs. 1500 as salary. Find the EOQ for the above production schedule.

Example-5
SMS Motor Company, the 2-wheeler manufacturer producing 2,50,000 units of mopeds per annum. The company is having its own tyre-manufacturing unit, which is producing tyres for internal consumption as well as acting as ‘Original Equipment Manufacturer’ for several 2-wheelers manufacturers in India. The tyre-manufacturing unit is in a possession to manufacture 20,000 tyres per day as far as any model is concerned and, will be in a position to produce 8,500 tyres per day as far as internal requirements are concerned. Whenever, the production operations starts on one specific type or model, again to produce a new model we have to re set the equipments which will costs Rs. 2500/ per setting. To hold one tyre in inventory, the company has to incur Rs. 100 per year. Assuming 250 working days per year, what will be the optimum manufacturing quantity?

Tags : Operations Management - Transportation / Assignment & Inventory Management
Last 30 days 1135 views












