Operations Management - Network Problems
Problem of Minimum Spanning Tree
Posted On :
Determine the minimum spanning tree for the following network.
Problem 1
Determine the minimum spanning tree for the following network.
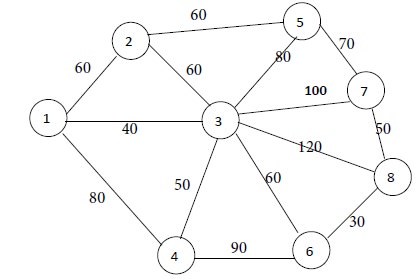
Solution
Step 1
First select node 1. (This is done arbitrarily)
Step 2
We have to connect node 1 to the nearest node. Nodes 2, 3 and 4 are adjacent to node 1. They are at distances of 60, 40 and 80 units from node Minimum of {60, 40, 80} = 40. Hence the shortest distance is 40. This corresponds to node 3. So we connect node 1 to node 3 by a thick line. This is Iteration No. 1.
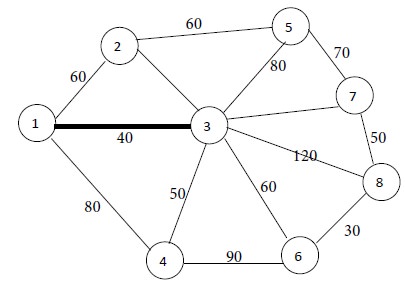
Iteration No. 1
Step 3
Now the connected nodes are 1 and 3. The remaining nodes are 2, 4, 5, 6, 7 and 8. Among them, nodes 2 and 4 are connected to node 1. They are at distances of 60 and 80 from node 1. Minimum of {60, 80} = 60. So the shortest distance is 60. Next, among the nodes 2, 4, 5, 6, 7 and 8, find out which nodes are connected to node 3. We find that all of them are connected to node 3. They are at distances of 60, 50, 80, 60, 100 and 120 from node 3. Minimum of {60, 50, 80, 60, 100, 120} = 50. Hence the shortest distance is 50.
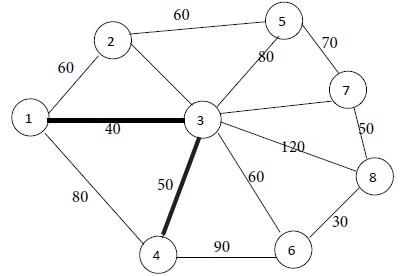
Iteration No. 2
Next go to step 3.
Now the connected nodes are 1, 3 and 4. The remaining nodes are 2, 5, 6, 7 and 8. Node 2 is at a distance of 60 from node 1. Nodes 5, 6, 7 and 8 are not adjacent to node 1. All of the nodes 2, 5, 6, 7 and 8 are adjacent to node 3. Among them, nodes 2 and 6 are nearer to node 3, with equal distance of 60.
Node 6 is adjacent to node 4, at a distance of 90. Now there is a tie between nodes 2 and 6. The tie can be broken arbitrarily. So we select node 2. Connect node 3 to Node 2 by a thick line. This is Iteration No. 3. 60
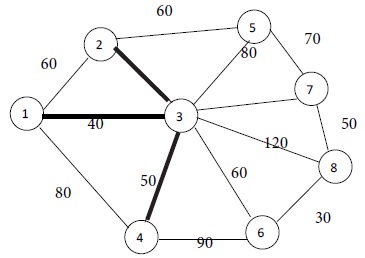
Iteration No. 3
We continue the above process
Now nodes 1, 2, 3 and 4 are connected. The remaining nodes are 5, 6, 7 and 8. None of them is adjacent to node 1. Node 5 is adjacent to node 2 at a distance of 60. Node 6 is at a distance of 60 from node 3. Node 6 is at a distance of 90 from node 4. There is a tie between nodes 5 and 6. We select node 5. Connect node 2 to node 5 by a thick line. This is Iteration No. 4.
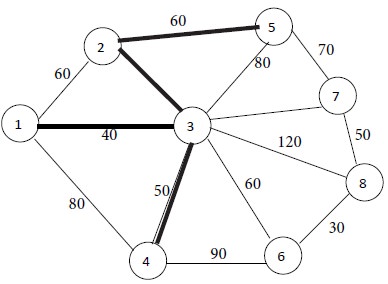
Iteration No. 4
Now nodes 1, 2, 3, 4 and 5 are connected. The remaining nodes are 6, 7 and 8. Among them, node 6 is at the shortest distance of 60 from node 3. So, connect node 3 to node 6 by a thick line. This is Iteration No. 5.
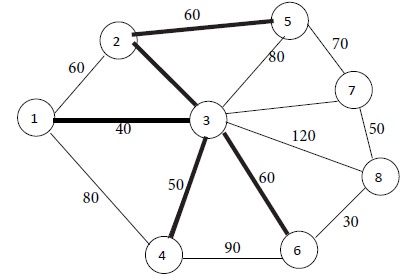
Iteration No. 5
Now nodes 1, 2, 3, 4, 5 and 6 are connected. The remaining nodes are 7 and 8. Among them, node 8 is at the shortest distance of 30 from node 6. Consequently we connect node 6 to node 8 by a thick line. This is Iteration No. 6.
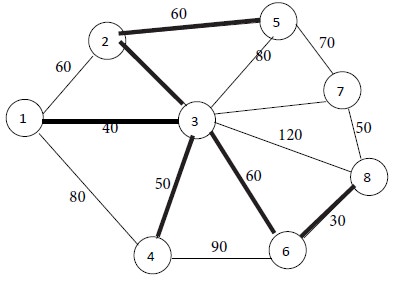
Iteration No. 6
Now nodes 1, 2, 3, 4, 5, 6 and 8 are connected. The remaining node is 7. It is at the shortest distance of 50 from node 8. So, connect node 8 to node 7 by a thick line. This is Iteration No.7.
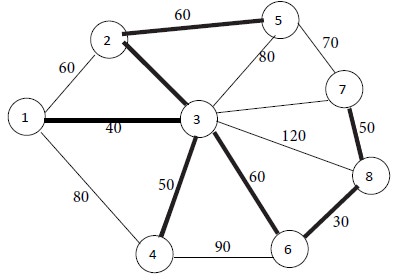
Iteration No. 7
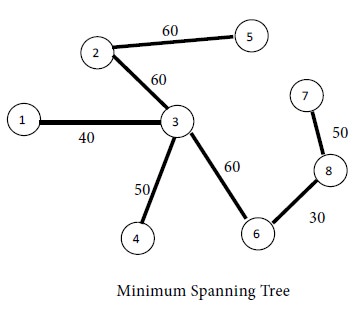
Now all the nodes 1, 2, 3, 4, 5, 6, 7 and 8 are connected by seven thick lines. Since no node is remaining, we have reached the stopping condition. Thus we obtain the following minimum spanning tree for the given network.
Determine the minimum spanning tree for the following network.

Solution
Step 1
First select node 1. (This is done arbitrarily)
Step 2
We have to connect node 1 to the nearest node. Nodes 2, 3 and 4 are adjacent to node 1. They are at distances of 60, 40 and 80 units from node Minimum of {60, 40, 80} = 40. Hence the shortest distance is 40. This corresponds to node 3. So we connect node 1 to node 3 by a thick line. This is Iteration No. 1.

Iteration No. 1
Step 3
Now the connected nodes are 1 and 3. The remaining nodes are 2, 4, 5, 6, 7 and 8. Among them, nodes 2 and 4 are connected to node 1. They are at distances of 60 and 80 from node 1. Minimum of {60, 80} = 60. So the shortest distance is 60. Next, among the nodes 2, 4, 5, 6, 7 and 8, find out which nodes are connected to node 3. We find that all of them are connected to node 3. They are at distances of 60, 50, 80, 60, 100 and 120 from node 3. Minimum of {60, 50, 80, 60, 100, 120} = 50. Hence the shortest distance is 50.
Among these nodes, it is seen that node 4 is
nearest to node 3.
Now we go to Step 2. We connect node 3 to node 4 by a thick line. This is Iteration No.2.
Now we go to Step 2. We connect node 3 to node 4 by a thick line. This is Iteration No.2.

Iteration No. 2
Next go to step 3.
Now the connected nodes are 1, 3 and 4. The remaining nodes are 2, 5, 6, 7 and 8. Node 2 is at a distance of 60 from node 1. Nodes 5, 6, 7 and 8 are not adjacent to node 1. All of the nodes 2, 5, 6, 7 and 8 are adjacent to node 3. Among them, nodes 2 and 6 are nearer to node 3, with equal distance of 60.
Node 6 is adjacent to node 4, at a distance of 90. Now there is a tie between nodes 2 and 6. The tie can be broken arbitrarily. So we select node 2. Connect node 3 to Node 2 by a thick line. This is Iteration No. 3. 60

We continue the above process
Now nodes 1, 2, 3 and 4 are connected. The remaining nodes are 5, 6, 7 and 8. None of them is adjacent to node 1. Node 5 is adjacent to node 2 at a distance of 60. Node 6 is at a distance of 60 from node 3. Node 6 is at a distance of 90 from node 4. There is a tie between nodes 5 and 6. We select node 5. Connect node 2 to node 5 by a thick line. This is Iteration No. 4.

Now nodes 1, 2, 3, 4 and 5 are connected. The remaining nodes are 6, 7 and 8. Among them, node 6 is at the shortest distance of 60 from node 3. So, connect node 3 to node 6 by a thick line. This is Iteration No. 5.

Now nodes 1, 2, 3, 4, 5 and 6 are connected. The remaining nodes are 7 and 8. Among them, node 8 is at the shortest distance of 30 from node 6. Consequently we connect node 6 to node 8 by a thick line. This is Iteration No. 6.

Now nodes 1, 2, 3, 4, 5, 6 and 8 are connected. The remaining node is 7. It is at the shortest distance of 50 from node 8. So, connect node 8 to node 7 by a thick line. This is Iteration No.7.

Now all the nodes 1, 2, 3, 4, 5, 6, 7 and 8 are connected by seven thick lines. Since no node is remaining, we have reached the stopping condition. Thus we obtain the following minimum spanning tree for the given network.
Tags : Operations Management - Network Problems
Last 30 days 992 views












