Operations Management - Network Problems
The Problem - Shortest Path Problem
Posted On :
Imagine a salesman or a milk vendor or a post man who has to cover certain previously earmarked places to perform his daily routines.
The Problem
Imagine a salesman or a milk vendor or a post man who has to cover certain previously earmarked places to perform his daily routines. It is assumed that all the places to be visited by him are connected well for a suitable mode of transport. He has to cover all the locations. While doing so, if he visits the same place again and again on the same day, it will be a loss of several resources such as time, money, etc. Therefore he shall place a constraint upon himself not to visit the same place again and again on the same day. He shall be in a position to determine a route which would enable him to cover all the locations, fulfilling the constraint.
The shortest route method aims to find how a person can travel from one location to another, keeping the total distance traveled to the minimum. In other words, it seeks to identify the shortest route to a series of destinations.
Example
Let us consider a real life situation involving a shortest route problem.
A leather manufacturing company has to transport the finished goods from the factory to the store house. The path from the factory to the store house is through certain intermediate stations as indicated in the following diagram. The company executive wants to identify the path with the shortest distance so as to minimize the transportation cost. The problem is to achieve this objective.
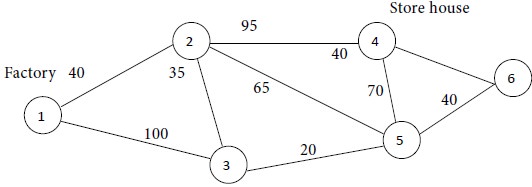
The shortest route technique can be used to minimize the total distance from a node designated as the starting node or origin to another node designated as the final node.
In the example under consideration, the origin is the factory and the final node is the store house.
The procedure consists of starting with a set containing a node and enlarging the set by choosing a node in each subsequent step.
Step 1
First, locate the origin. Then, find the node nearest to the origin. Mark the distance between the origin and the nearest node in a box by the side of that node.
In some cases, it may be necessary to check several paths to find the nearest node.
Step 2
Imagine a salesman or a milk vendor or a post man who has to cover certain previously earmarked places to perform his daily routines. It is assumed that all the places to be visited by him are connected well for a suitable mode of transport. He has to cover all the locations. While doing so, if he visits the same place again and again on the same day, it will be a loss of several resources such as time, money, etc. Therefore he shall place a constraint upon himself not to visit the same place again and again on the same day. He shall be in a position to determine a route which would enable him to cover all the locations, fulfilling the constraint.
The shortest route method aims to find how a person can travel from one location to another, keeping the total distance traveled to the minimum. In other words, it seeks to identify the shortest route to a series of destinations.
Example
Let us consider a real life situation involving a shortest route problem.
A leather manufacturing company has to transport the finished goods from the factory to the store house. The path from the factory to the store house is through certain intermediate stations as indicated in the following diagram. The company executive wants to identify the path with the shortest distance so as to minimize the transportation cost. The problem is to achieve this objective.

Linkages from Factory to Store house
The shortest route technique can be used to minimize the total distance from a node designated as the starting node or origin to another node designated as the final node.
In the example under consideration, the origin is the factory and the final node is the store house.
Steps In The Shortest Route Technique
The procedure consists of starting with a set containing a node and enlarging the set by choosing a node in each subsequent step.
Step 1
First, locate the origin. Then, find the node nearest to the origin. Mark the distance between the origin and the nearest node in a box by the side of that node.
In some cases, it may be necessary to check several paths to find the nearest node.
Step 2
Repeat the above process until the nodes in the entire network have been accounted for. The last distance placed in a box by the side of the ending node will be the distance of the shortest route. We note that the distances indicated in the boxes by each node constitute the shortest route to that node. These distances are used as intermediate results in determining the next nearest node.
Tags : Operations Management - Network Problems
Last 30 days 654 views












