Home | ARTS | Operations Management
|
Simplex Algorithm - Linear Programming – Problem Solving [SIMPLEX METHOD]
Operations Management - Introduction to Operations Research
Simplex Algorithm - Linear Programming – Problem Solving [SIMPLEX METHOD]
Posted On :
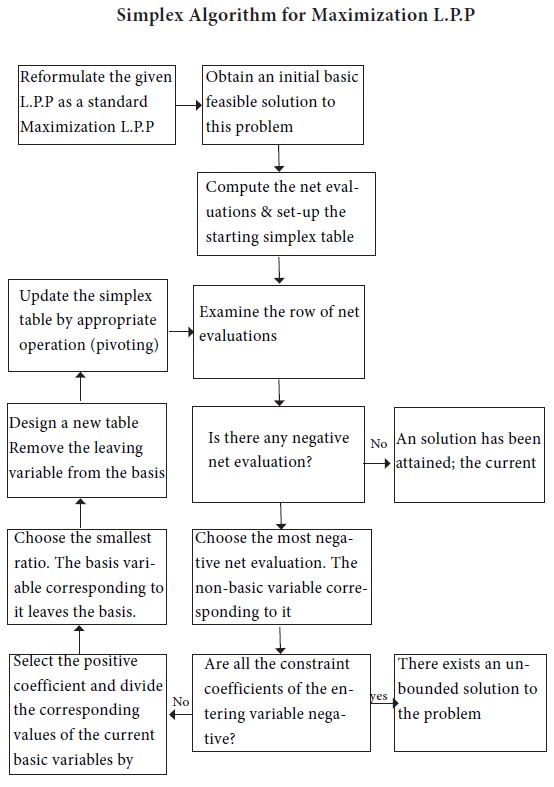
Check whether the objective function of the given L.P.P. is to be maximized or minimized.
Simplex Algorithm
Check whether the objective function of the given L.P.P. is to be maximized or minimized.
If it is to be minimized then convert it into a problem of maximizing it by using the result
Minimum= -Maximum (-z)
Check whether all ‘b’ values are non-negative. If any one of b is negative then multiply the corresponding inequality constraints by –1, so as to get all b values as non-negative.
Convert all the in equations of the constraints into equations by introducing slack and/or surplus variables in the constraints. Put the costs of these variables equal to zero in the objective function, if the variables are slack variables. If surplus / artificial variables are added,
Obtain an initial basic feasible solution to the problem in the form Xb=B^-1 b and put it in the first column of the simplex table.
Compute the net evaluations zj-cj (j=1,2…n) by using the relation,
Zj-Cj=CB yj-cj.
Examine the sign zj-cj.
i. If all values are >=0, then initial basic feasible solution is an optimum feasible solution.
ii.
If at
least one value < 0, go to next step.
If there is more than one negative value, then choose most negative.
Compute the ratio
{xb/yi, yi>0,I=1,2…. m} and choose the minimum of them.
The common element in the kth row and rth column is known as the leading element (pivotal element) of the table.
Convert the leading element to unity by dividing its row by the leading element itself and all other elements in its column to zeros.
Go to step 5 and repeat the process until either an optimum solution is obtained or there is an indication of unbounded solution.
Step 1
Check whether the objective function of the given L.P.P. is to be maximized or minimized.
If it is to be minimized then convert it into a problem of maximizing it by using the result
Step 2
Check whether all ‘b’ values are non-negative. If any one of b is negative then multiply the corresponding inequality constraints by –1, so as to get all b values as non-negative.
Step 3
Convert all the in equations of the constraints into equations by introducing slack and/or surplus variables in the constraints. Put the costs of these variables equal to zero in the objective function, if the variables are slack variables. If surplus / artificial variables are added,
Step 4
Obtain an initial basic feasible solution to the problem in the form Xb=B^-1 b and put it in the first column of the simplex table.
Step 5
Compute the net evaluations zj-cj (j=1,2…n) by using the relation,
Zj-Cj=CB yj-cj.
Examine the sign zj-cj.
i. If all values are >=0, then initial basic feasible solution is an optimum feasible solution.
Step 6
If there is more than one negative value, then choose most negative.
Step 7
Compute the ratio
{xb/yi, yi>0,I=1,2…. m} and choose the minimum of them.
The common element in the kth row and rth column is known as the leading element (pivotal element) of the table.
Step 8
Convert the leading element to unity by dividing its row by the leading element itself and all other elements in its column to zeros.
Step 9
Go to step 5 and repeat the process until either an optimum solution is obtained or there is an indication of unbounded solution.

Tags : Operations Management - Introduction to Operations Research
Last 30 days 1007 views












