Research Methodology - Correlation And Regression Analysis
TYPES OF CORRELATION - Correlation And Regression Analysis
Posted On :
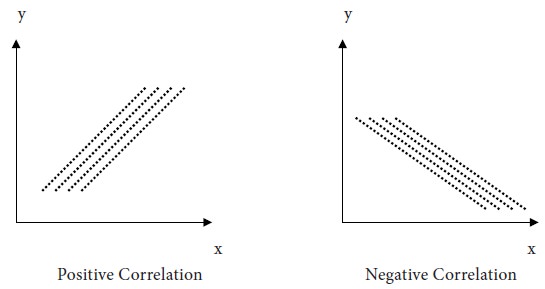
If two variables x and y move in the same direction, we say that there is a positive correlation between them.
TYPES OF
CORRELATION
If two variables x and y move in the same direction, we say that there is a positive correlation between them. In this case, when the value of one variable increases, the value of the other variable also increases and when the value of one variable decreases, the value of the other variable also decreases. Eg. The age and height of a child.
If two variables x and y move in opposite directions, we say that there is a negative correlation between them. i.e., when the value of one variable increases, the value of the other variable decreases and vice versa. Eg. The price and demand of a normal good.
The following diagrams illustrate positive and negative correlations between x and y.
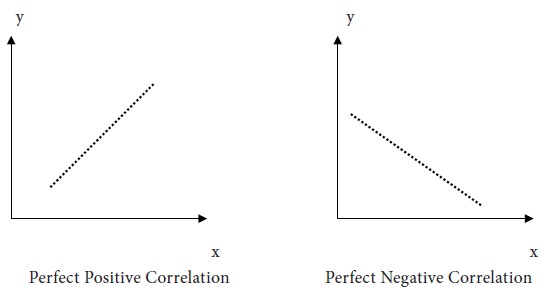
If changes in two variables are in the same direction and the changes are in equal proportion, we say that there is a perfect positive correlation between them.
If changes in two variables are in opposite directions and the absolute values of changes are in equal proportion, we say that there is a perfect negative correlation between them.
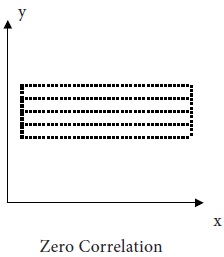
If there is no relationship between the two variables, then the variables are said to be independent. In this case the correlation between the two variables is zero.
If the quantum of change in one variable always bears a constant ratio to the quantum of change in the other variable, we say that the two variables have a linear correlation between them.
The coefficient of correlation between two variables X, Y is a measure of the degree of association (i.e., strength of relationship) between them. The coefficient of correlation is usually denoted by ‘r’.
Let N denote the number of pairs of observations of two variables X and Y. The correlation coefficient r between X and Y is defined by
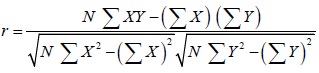
Positive correlation
If two variables x and y move in the same direction, we say that there is a positive correlation between them. In this case, when the value of one variable increases, the value of the other variable also increases and when the value of one variable decreases, the value of the other variable also decreases. Eg. The age and height of a child.
Negative correlation
If two variables x and y move in opposite directions, we say that there is a negative correlation between them. i.e., when the value of one variable increases, the value of the other variable decreases and vice versa. Eg. The price and demand of a normal good.
The following diagrams illustrate positive and negative correlations between x and y.

Perfect Positive Correlation
If changes in two variables are in the same direction and the changes are in equal proportion, we say that there is a perfect positive correlation between them.
Perfect Negative Correlation
If changes in two variables are in opposite directions and the absolute values of changes are in equal proportion, we say that there is a perfect negative correlation between them.

Zero Correlation
If there is no relationship between the two variables, then the variables are said to be independent. In this case the correlation between the two variables is zero.

Linear Correlation
If the quantum of change in one variable always bears a constant ratio to the quantum of change in the other variable, we say that the two variables have a linear correlation between them.
Coefficient of Correlation
The coefficient of correlation between two variables X, Y is a measure of the degree of association (i.e., strength of relationship) between them. The coefficient of correlation is usually denoted by ‘r’.
Karl Pearson’s Coefficient Of Simple Correlation:
Let N denote the number of pairs of observations of two variables X and Y. The correlation coefficient r between X and Y is defined by
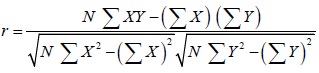
This formula is suitable for solving problems with
hand calculators. To apply this formula, we have to calculate ∑ X,∑Y, ∑XY, ∑X2,
∑Y2.
Tags : Research Methodology - Correlation And Regression Analysis
Last 30 days 1254 views












