Home | ARTS | Operations Management
|
Linear Programming – Problem formulation [Mathematical Modeling]
Operations Management - Introduction to Operations Research
Linear Programming – Problem formulation [Mathematical Modeling]
Posted On :
We have briefly discussed the meaning of models, various types of models; we are particularly more interested in the mathematical models.
Linear Programming
– Problem formulation [Mathematical Modeling]
We have briefly discussed the meaning of models, various types of models; we are particularly more interested in the mathematical models. Let us consider the following situation pertaining to a furniture manufacturing firm.
A furniture company manufactures desks and chairs. There are four departments namely carpentry, upholstery, painting and varnishing with capacities as given below:
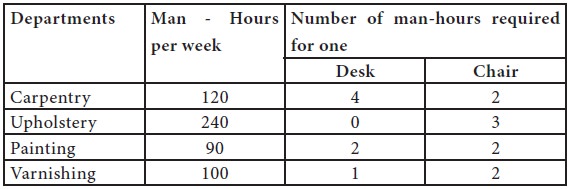
Assuming that raw materials are available in adequate quantities and the manufacturer wishes to know how many desks and chairs he should produce. He enjoys a good market share. The contribution from a desk is Rs.40/- and that from a chair is Rs.25/-
Let us develop the mathematical model of the given situation as follows:
Let us say, we want to produce X1 units of Desks and X2 Units of Chairs.
By producing one unit of desk, the manufacturer gets Rs. 40/- as profit and for chairs, he gets Rs. 25/-
Therefore, the total profits = 40X1 + 25X2
Obviously, the objective of the firm, therefore, is Maximize the total profits, which is expressed as a mathematical expression (function) as
Max Z = 40X1 + 25X2
However, in achieving the objective, the firm faces several constraints. The first constraint is from the carpentry section; to produce, one unit of desk, it needs 4 hours from this section and for producing chairs, and this section needs to spend 2 hours. However, this section, in total, available, only for 120 hours in the week.
Thus, the first constraint is formulated as follows:
4X1 + 2X2 <= 120 ………………….. (1)
Upholstery section’s service is needed only for producing chairs and to produce one unit of chair, this section has to spend 3 hours and its maximum availability is 240 hours per
3X2 <= 240 ………………….. (2)
Similarly, the painting section’s availability per week is limited to 90 hours. To produce a desk or chair, this section has to spend 2 hours for each unit. Hence, the constraint for painting section is,
2X1 + 2X2 <= 90 ………………….. (3)
Finally, the varnishing section’s services are needed for both the products, and it is limited to 100 hours per week. To produce a desk, it needs to spend 1 hour and to produce a chair; it has to spend 2 hours. Thus, the constraint for varnishing section is,
X1 + 2X2 <= 100 ………………….. (4)
Obviously, the production quantities like number of desks (X1) and number of chairs (X2) cannot be negative; we add two more constraints to this situation. They are
X1 ≥ 0 and X2 ≥0
Therefore, the mathematical formulation of the given situation is
Max Z = 40X1 + 25X2
Subject to
4X1 + 2X2 <= 120
3X2 <= 240
2X1 + 2X2 <= 90
X1 + 2X2 <= 100
X1 ≥ 0 and X2 ≥0
Therefore by reading,
Max Z = 40X1 + 25X2
Subject to
4X1 + 2X2 <= 120
3X2 <= 240
2X1 + 2X2 <= 90
X1 + 2X2 <= 100
X1 ≥ 0 and X2 ≥0
The reader can understood that the firm has to decide the quantities to be produced in desks and chairs, so as to make the maximize profit / contribution and achieving this objective is subject to 4 constrains – availability of raw materials from its 4 departments.
Thus, the mathematical model summarizes the information provided in the context / situations in terms of mathematical symbols and notations. We will take few more examples.
Example1: Distillers Production Schedule
M/S. RK Distillers Ltd (RKDL) has two bottling plants, one located at Pondicherry and the other at Chennai. Each plant produces three brands of liquor products, Challenge, Royal and Salute under the job order contract to the leading liquor baron MB Distillers and Bottlers Ltd (MBDL). The number of cases produced per day is as follows:
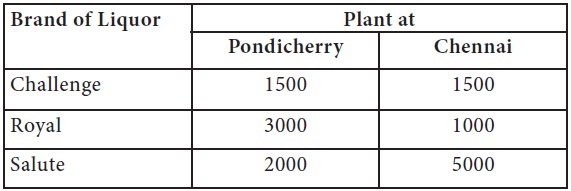
As per the sales forecast given by the marketing team, MBDL expects a minimum of 30000 cases of Challenge, 40000 cases of Royal and 44000 cases of Salute from RKDL for the next fortnight. The operating costs per day for plants at Chennai and Pondicherry are 600 and 450 thousands per day. How many days each plant should run to fulfill the orders for the next fortnight? [You can assume that the factory runs all the 7 days in a week-since there is a shift system to take care of weekly off]
Solution
Let X1 be the number of days Chennai plant to be operated and X2 be the number of days Pondicherry plant should run.
The firm aims to reduce the overall operating cost arising out operations subject to fulfilling the market demand.
Therefore, the objective is to minimize the total operating cost; to operate the Chennai plant for X1 days, the firm has to incur 600X1+ 450X2
Min Z = 600X1 + 450X2
Subject to
1500X1 + 1500X2 >= 30,000
We have briefly discussed the meaning of models, various types of models; we are particularly more interested in the mathematical models. Let us consider the following situation pertaining to a furniture manufacturing firm.
A furniture company manufactures desks and chairs. There are four departments namely carpentry, upholstery, painting and varnishing with capacities as given below:

Assuming that raw materials are available in adequate quantities and the manufacturer wishes to know how many desks and chairs he should produce. He enjoys a good market share. The contribution from a desk is Rs.40/- and that from a chair is Rs.25/-
Let us develop the mathematical model of the given situation as follows:
Let us say, we want to produce X1 units of Desks and X2 Units of Chairs.
By producing one unit of desk, the manufacturer gets Rs. 40/- as profit and for chairs, he gets Rs. 25/-
Therefore, the profits from desks | = 40 * X1 |
Profits from chairs | = 25 * X2 |
Therefore, the total profits = 40X1 + 25X2
Obviously, the objective of the firm, therefore, is Maximize the total profits, which is expressed as a mathematical expression (function) as
Max Z = 40X1 + 25X2
However, in achieving the objective, the firm faces several constraints. The first constraint is from the carpentry section; to produce, one unit of desk, it needs 4 hours from this section and for producing chairs, and this section needs to spend 2 hours. However, this section, in total, available, only for 120 hours in the week.
Thus, the first constraint is formulated as follows:
4X1 + 2X2 <= 120 ………………….. (1)
Upholstery section’s service is needed only for producing chairs and to produce one unit of chair, this section has to spend 3 hours and its maximum availability is 240 hours per
3X2 <= 240 ………………….. (2)
Similarly, the painting section’s availability per week is limited to 90 hours. To produce a desk or chair, this section has to spend 2 hours for each unit. Hence, the constraint for painting section is,
2X1 + 2X2 <= 90 ………………….. (3)
Finally, the varnishing section’s services are needed for both the products, and it is limited to 100 hours per week. To produce a desk, it needs to spend 1 hour and to produce a chair; it has to spend 2 hours. Thus, the constraint for varnishing section is,
X1 + 2X2 <= 100 ………………….. (4)
Obviously, the production quantities like number of desks (X1) and number of chairs (X2) cannot be negative; we add two more constraints to this situation. They are
X1 ≥ 0 and X2 ≥0
Therefore, the mathematical formulation of the given situation is
Max Z = 40X1 + 25X2
Subject to
4X1 + 2X2 <= 120
3X2 <= 240
2X1 + 2X2 <= 90
X1 + 2X2 <= 100
X1 ≥ 0 and X2 ≥0
Therefore by reading,
Max Z = 40X1 + 25X2
Subject to
4X1 + 2X2 <= 120
3X2 <= 240
2X1 + 2X2 <= 90
X1 + 2X2 <= 100
X1 ≥ 0 and X2 ≥0
The reader can understood that the firm has to decide the quantities to be produced in desks and chairs, so as to make the maximize profit / contribution and achieving this objective is subject to 4 constrains – availability of raw materials from its 4 departments.
Thus, the mathematical model summarizes the information provided in the context / situations in terms of mathematical symbols and notations. We will take few more examples.
Example1: Distillers Production Schedule
M/S. RK Distillers Ltd (RKDL) has two bottling plants, one located at Pondicherry and the other at Chennai. Each plant produces three brands of liquor products, Challenge, Royal and Salute under the job order contract to the leading liquor baron MB Distillers and Bottlers Ltd (MBDL). The number of cases produced per day is as follows:

As per the sales forecast given by the marketing team, MBDL expects a minimum of 30000 cases of Challenge, 40000 cases of Royal and 44000 cases of Salute from RKDL for the next fortnight. The operating costs per day for plants at Chennai and Pondicherry are 600 and 450 thousands per day. How many days each plant should run to fulfill the orders for the next fortnight? [You can assume that the factory runs all the 7 days in a week-since there is a shift system to take care of weekly off]
Solution
Let X1 be the number of days Chennai plant to be operated and X2 be the number of days Pondicherry plant should run.
The firm aims to reduce the overall operating cost arising out operations subject to fulfilling the market demand.
Therefore, the objective is to minimize the total operating cost; to operate the Chennai plant for X1 days, the firm has to incur 600X1+ 450X2
Min Z = 600X1 + 450X2
Subject to
1500X1 + 1500X2 >= 30,000
3000X1 + 1000X2 >= 40,000
2000X1 + 5000X2 >= 44000
Where, X1, X2 >= 0
Example2: Product Mix Decision
A company producing a standard line and a deluxe line of dish washers has the following time requirements (in minutes) in departments where either model can be processed.
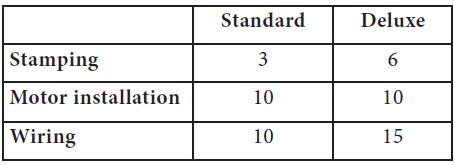
The standard models contribute Rs. 20 each and the deluxe Rs. 30 each to profits. Because the company produces other items that share resources used to make the dishwashers, the stamping machine is available only 30 minutes per hour, on average. The motor installation production line has 60 minutes available each hour. There are two lines for wiring, so the time availability is 90 minutes per hour. Write the formulation for this linear program
Solution
Let X = number of standard dishwashers produced per hour Y = number of deluxe dishwashers produced per hour
Therefore, the objective is to maximize the total contribution from these two products.
Thus, it is written as
Max Z= 20X + 30 Y
This contribution realization is subject to the following constraints;
And obviously, X & Y cannot be negative quantities, hence, X>=0 & Y>=0
Example3: Product Mix Decision @ Whoppy Soft Drinks
The production manager for the Whoppy soft drink company is considering the production of 2 kinds of soft drinks: regular (R) and diet (D). The company operates one “8 hour” shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are Rs.3.00 per case and profits for diet soft drink are Rs.2.00 per case. Write the formulation for this linear program.
Solution
Let R = number of regular drinks produced per days D = number of diet drinks produced per days
Therefore, the objective is to maximize the total contribution
Thus, it is written as
Max Z= 3R + 2D
This contribution realization is subject to the following constraints;
2R + 4D ≤ 480 -------------- (Production time constraint)
5R + 3D ≤ 675 -------------- (Syrup availability constraint)
And obviously, R & D cannot be negative quantities, hence, R>=0 & D>=0
Example4: Sales Mix Decision for computer retail sales
A computer retail store sells two types of flat screen monitors: 17 inches and 19 inches, with a profit contribution of Rs. 300 and Rs. 250, respectively. The monitors are ordered each week from an outside supplier. As an added feature, the retail store installs on each monitor a privacy filter that narrows the viewing angle so that only persons sitting directly in front of the monitor are able to see on-screen data. Each 19” monitor consumes about 30 minutes of installation time, while each 17” monitor requires about 10 minutes of installation time. The retail store has approximately 40 hours of labor time available each week. The total combined demand for both monitors is at least 40 monitors each week. How many units of each monitor should the retail store order each week to maximize its weekly profits and meet its weekly demand?
Solution
Let
X1 = number of 17 inches monitor to be ordered per week
X2 = number of 19 inches monitor to be ordered per week
Therefore, the objective of the retail service firm is to maximize the total contribution from these computer monitor sales. The retail firm gets Rs. 300 and Rs. 250 per monitor for 17 and 19 inches respectively, therefore, the objective function arrived as follows:
Max Z= 300 X1 + 250 X2
This contribution realization is subject to the following constraints;
monitor per week constraint)
And obviously, X1 & X2 cannot be negative quantities, hence, X1>=0 & X2>=0
Exercises [Try on your own]
1. A furniture store produces beds and desks for college students. The production process requires assembly and painting. Each bed requires 6 hours of assembly and 4 hours of painting. Each desk requires 4 hours of assembly and 8 hours of painting. There are 40 hours of assembly time and 45 hours of painting time available each week. Each bed generates $35 of profit and each desk generates $45 of profit. As a result of a labor strike, the furniture store is
2. A bank is attempting to determine where its assets should be allocated in order to maximize its annual return. At present, $750,000 is available for investment in three types of mutual funds: A, B, and C. The annual rate of return on each type of fund is as follows: fund A, 15%; fund B, 12%; fund C; 13%. The bank’s manager has placed the following restrictions on the bank’s portfolio:
1. No more than 20% of the total amount invested may be in fund A
2. The amount invested in fund B cannot exceed the amount invested in fund C
Determine the optimal allocation that maximizes the bank’s annual return.
2000X1 + 5000X2 >= 44000
Where, X1, X2 >= 0
Example2: Product Mix Decision
A company producing a standard line and a deluxe line of dish washers has the following time requirements (in minutes) in departments where either model can be processed.

The standard models contribute Rs. 20 each and the deluxe Rs. 30 each to profits. Because the company produces other items that share resources used to make the dishwashers, the stamping machine is available only 30 minutes per hour, on average. The motor installation production line has 60 minutes available each hour. There are two lines for wiring, so the time availability is 90 minutes per hour. Write the formulation for this linear program
Solution
Let X = number of standard dishwashers produced per hour Y = number of deluxe dishwashers produced per hour
Therefore, the objective is to maximize the total contribution from these two products.
Max Z= 20X + 30 Y
This contribution realization is subject to the following constraints;
3X + 6Y ≤ 30 -------------- | (Stamping
Machine constraint) |
10X + 10Y ≤ 60
-------------- | (Motor
installation constraint) |
10X + 15Y ≤ 90
-------------- | (Wiring
machine constraint) |
And obviously, X & Y cannot be negative quantities, hence, X>=0 & Y>=0
Example3: Product Mix Decision @ Whoppy Soft Drinks
The production manager for the Whoppy soft drink company is considering the production of 2 kinds of soft drinks: regular (R) and diet (D). The company operates one “8 hour” shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are Rs.3.00 per case and profits for diet soft drink are Rs.2.00 per case. Write the formulation for this linear program.
Solution
Let R = number of regular drinks produced per days D = number of diet drinks produced per days
Therefore, the objective is to maximize the total contribution
Thus, it is written as
Max Z= 3R + 2D
This contribution realization is subject to the following constraints;
2R + 4D ≤ 480 -------------- (Production time constraint)
5R + 3D ≤ 675 -------------- (Syrup availability constraint)
And obviously, R & D cannot be negative quantities, hence, R>=0 & D>=0
Example4: Sales Mix Decision for computer retail sales
A computer retail store sells two types of flat screen monitors: 17 inches and 19 inches, with a profit contribution of Rs. 300 and Rs. 250, respectively. The monitors are ordered each week from an outside supplier. As an added feature, the retail store installs on each monitor a privacy filter that narrows the viewing angle so that only persons sitting directly in front of the monitor are able to see on-screen data. Each 19” monitor consumes about 30 minutes of installation time, while each 17” monitor requires about 10 minutes of installation time. The retail store has approximately 40 hours of labor time available each week. The total combined demand for both monitors is at least 40 monitors each week. How many units of each monitor should the retail store order each week to maximize its weekly profits and meet its weekly demand?
Solution
Let
X1 = number of 17 inches monitor to be ordered per week
X2 = number of 19 inches monitor to be ordered per week
Therefore, the objective of the retail service firm is to maximize the total contribution from these computer monitor sales. The retail firm gets Rs. 300 and Rs. 250 per monitor for 17 and 19 inches respectively, therefore, the objective function arrived as follows:
Max Z= 300 X1 + 250 X2
This contribution realization is subject to the following constraints;
10X1 + 30X2 ≤ 2400 | -------------- (Labor time constraint) |
X1 + X2 ≥ 40 -------------- | (Market demand for the computer |
monitor per week constraint)
And obviously, X1 & X2 cannot be negative quantities, hence, X1>=0 & X2>=0
Exercises [Try on your own]
1. A furniture store produces beds and desks for college students. The production process requires assembly and painting. Each bed requires 6 hours of assembly and 4 hours of painting. Each desk requires 4 hours of assembly and 8 hours of painting. There are 40 hours of assembly time and 45 hours of painting time available each week. Each bed generates $35 of profit and each desk generates $45 of profit. As a result of a labor strike, the furniture store is
2. A bank is attempting to determine where its assets should be allocated in order to maximize its annual return. At present, $750,000 is available for investment in three types of mutual funds: A, B, and C. The annual rate of return on each type of fund is as follows: fund A, 15%; fund B, 12%; fund C; 13%. The bank’s manager has placed the following restrictions on the bank’s portfolio:
1. No more than 20% of the total amount invested may be in fund A
2. The amount invested in fund B cannot exceed the amount invested in fund C
Determine the optimal allocation that maximizes the bank’s annual return.
Tags : Operations Management - Introduction to Operations Research
Last 30 days 3101 views












