Research Methodology - Experiments
Formal Experimental Designs - Experiments
Posted On :
This design involves only two principles i.e., the principle of replication and the principle of randomization of experimental designs.
Formal Experimental Design
This design involves only two principles i.e., the principle of replication and the principle of randomization of experimental designs. Among all other designs this is the simpler and easier because it’s procedure and analysis are simple. The important characteristic of this design is that the subjects are randomly assigned to experimental treatments. For example, if the researcher has 20 subjects and if he wishes to test 10 under treatment A and 10 under treatment B, the randomization process gives every possible group of 10 subjects selected from a set of 20 an equal opportunity of being assigned to treatment A and treatment B. One way analysis of variance (one way ANOVA) is used to analyze such a design.
R. B. Design is an improvement over the C.R. design. In the R .B. Design, the principle of local control can be applied along with the other two principles of experimental designs. In the R.B. design, subjects are first divided into groups, known as blocks, such that within each group the subjects are relatively homogenous in respect to some selected variable. The number of subjects in a given block would be randomly assigned to each treatment. Blocks are the levels at which we hold the extraneous factor fixed, so that its contribution to the total variability of data can be measured. The main feature of the R.B. design is that, in this, each treatment appears the same number of times in each block. This design is analyzed by the two-way analysis of variance (two-way ANOVA) technique.
The Latin squares design (L.S design) is an experimental design which is very frequently used in agricultural research. Since agriculture depends upon nature to a large extent, the condition of research and investigation in agriculture is different than the other studies. For example, an experiment has to be made through which the effects of fertilizers on the yield of a certain crop, say wheat, are to be judged. In this situation, the varying fertility of the soil in different blocks in which the experiment has to be performed must be taken into consideration; otherwise the results obtained may not be very dependable because the output happens to be the effects of not only of fertilizers, but also of the effect of fertility of soil. Similarly there may be the impact of varying seeds of the yield. In order to overcome such difficulties, the L.S. design is used when there are two major extraneous factors such as the varying soil fertility and varying seeds. The Latin square design is such that each fertilizer will appear five times but will be used only once in each row and in each column of the design. In other words, in this design, the treatment is so allocated among the plots that no treatment occurs more than once in any one row or any one column. This experiment can be shown with the help of the following diagram:
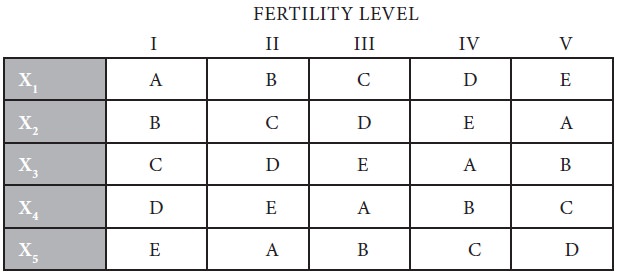
From the above diagram, it is clear that in L.S. design the field is divided into as many blocks as there are varieties of fertilizers. Then, each block is again divided into as many parts as there are varieties of fertilizers in such a way that each of the fertilizer variety is used in each of the block only once. The analysis of L.S. design is very similar to the two-way ANOVA technique.
Factorial designs are used in experiments where the effects of varying more than one factor are to be determined. These designs are used more in economic and social matters where usually a large number of factors affect a particular problem. Factorial designs are usually of two types:
1. Simple factorial designs and
When the experiments with more than two factors at a time are conducted, it involves the use of complex factorial designs. A design which considers three or more independent variables simultaneously is called a complex factorial design. In case of three factors with one experimental variable, two treatments and two levels, complex factorial design will contain a total of eight cells. This can be seen through the following diagram:
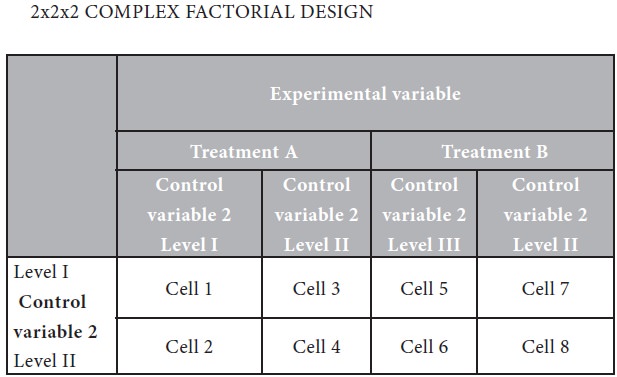
A pictorial presentation is given of the design shown above in the following:
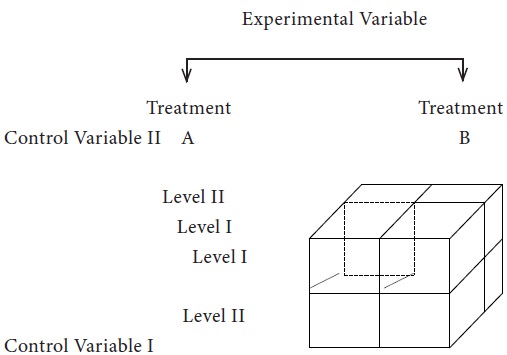
The dotted line cell in this diagram corresponds to cell I of the above stated 2x2x2 design and is for treatment A, level I of the control variable 1, and levelIi of the control variable 2. From this design, it is possible to determine the main effects for three variables i.e., one experimental and true control variables. The researcher can also determine the interaction between each possible pair of variables (such interactions are called ‘first order interactions’) and interaction between variable taken in triplets (such interactions are called second order interactions). In case of a 2x2x2 design, the further given first order interactions are possible:
There will be one second order interaction as well in the given design (it is between all the three variables i.e., EV x CV 1 x CV 2).
To determine the main effect for the experimental variable, the researcher must necessarily compare the combined mean of data in cells 1, 2, 3 and 4 for Treatment A with the combined mean of data in cells 5,6,7 and 8 for Treatment B. In this way the main effect of experimental variable, independent of control variable 1 and variable 2, is obtained. Similarly, the main effect for control variable 1, independent experimental variable and control variable 2, is obtained if we compare the combined mean of data in cells 1, 3, 5 and 7 with the combined mean of data in cells 2, 4, 6 and 8 of our 2x2x2 factorial design. On similar lines, one can determine the effect of control variable 2 independent of experimental variable and control variable 1, if the combined mean of data in cells 1,2,5 and 6 are compared with the combined mean of data in cells 3,4,7 and 8.
To obtain the first order interaction, say, for EV x CV 1 in the above stated design, the researcher must necessarily ignore control variable 2 for which purpose he may develop 2x2 design from the 2x2x2 design by combining the data of the relevant cells of the latter design as has been shown on next page:
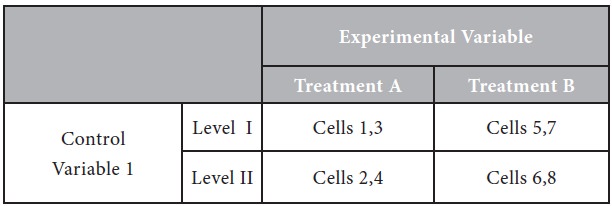
Similarly, the researcher can determine other first order interactions. The analysis of the first order interaction in the manner described above is essentially a simple factorial analysis as only two variables are considered at a time and the remaining ones are ignored. But the analysis of the second order interaction would not ignore one of the three independent variables in case of a 2x2x2 design. The analysis would be termed as a complex factorial analysis.
It may, however, be remembered that the complex factorial design need not necessarily be of 2x2x2 type design, but can be generalized to any number and combinations of experimental and control independent variables. Of course, the greater the number of independent variables included in a complex factorial design, the higher the order of the interaction analysis possible. But the overall task goes on becoming more and more complicated with the inclusion of more and more independent variables in our design.
Factorial designs are used mainly because of the two advantages -
(i) They provide equivalent accuracy (as happens in the case of experiments with only one factor) with less labour and as such are source of economy. Using factorial designs, we can determine the effects of two (in simple factorial design) or more (in case of complex factorial design) factors (or variables) in one single experiment. (ii) they permit various other comparisons of interest. For example, they give information about such effects which cannot be obtained by treating one single factor at a time. The determination of interaction effects is possible in case of factorial designs.
Completely randomized design:
This design involves only two principles i.e., the principle of replication and the principle of randomization of experimental designs. Among all other designs this is the simpler and easier because it’s procedure and analysis are simple. The important characteristic of this design is that the subjects are randomly assigned to experimental treatments. For example, if the researcher has 20 subjects and if he wishes to test 10 under treatment A and 10 under treatment B, the randomization process gives every possible group of 10 subjects selected from a set of 20 an equal opportunity of being assigned to treatment A and treatment B. One way analysis of variance (one way ANOVA) is used to analyze such a design.
Randomized block design:
R. B. Design is an improvement over the C.R. design. In the R .B. Design, the principle of local control can be applied along with the other two principles of experimental designs. In the R.B. design, subjects are first divided into groups, known as blocks, such that within each group the subjects are relatively homogenous in respect to some selected variable. The number of subjects in a given block would be randomly assigned to each treatment. Blocks are the levels at which we hold the extraneous factor fixed, so that its contribution to the total variability of data can be measured. The main feature of the R.B. design is that, in this, each treatment appears the same number of times in each block. This design is analyzed by the two-way analysis of variance (two-way ANOVA) technique.
Latin squares design:
The Latin squares design (L.S design) is an experimental design which is very frequently used in agricultural research. Since agriculture depends upon nature to a large extent, the condition of research and investigation in agriculture is different than the other studies. For example, an experiment has to be made through which the effects of fertilizers on the yield of a certain crop, say wheat, are to be judged. In this situation, the varying fertility of the soil in different blocks in which the experiment has to be performed must be taken into consideration; otherwise the results obtained may not be very dependable because the output happens to be the effects of not only of fertilizers, but also of the effect of fertility of soil. Similarly there may be the impact of varying seeds of the yield. In order to overcome such difficulties, the L.S. design is used when there are two major extraneous factors such as the varying soil fertility and varying seeds. The Latin square design is such that each fertilizer will appear five times but will be used only once in each row and in each column of the design. In other words, in this design, the treatment is so allocated among the plots that no treatment occurs more than once in any one row or any one column. This experiment can be shown with the help of the following diagram:

From the above diagram, it is clear that in L.S. design the field is divided into as many blocks as there are varieties of fertilizers. Then, each block is again divided into as many parts as there are varieties of fertilizers in such a way that each of the fertilizer variety is used in each of the block only once. The analysis of L.S. design is very similar to the two-way ANOVA technique.
Factorial design:
Factorial designs are used in experiments where the effects of varying more than one factor are to be determined. These designs are used more in economic and social matters where usually a large number of factors affect a particular problem. Factorial designs are usually of two types:
1. Simple factorial designs and
2. Complex factorial designs.
In simple factorial design, the effects of varying two factors on the dependent variable are considered but when an experiment is done with more than two factors, complex factorial designs are used. Simple factorial design is also termed as a ‘two-factor-factorial design,’ whereas complex factorial design is known as ‘multi-factor-factorial design.
Simple factorial design:
In simple factorial design, the effects of varying two factors on the dependent variable are considered but when an experiment is done with more than two factors, complex factorial designs are used. Simple factorial design is also termed as a ‘two-factor-factorial design,’ whereas complex factorial design is known as ‘multi-factor-factorial design.
Complex factorial designs:
When the experiments with more than two factors at a time are conducted, it involves the use of complex factorial designs. A design which considers three or more independent variables simultaneously is called a complex factorial design. In case of three factors with one experimental variable, two treatments and two levels, complex factorial design will contain a total of eight cells. This can be seen through the following diagram:

A pictorial presentation is given of the design shown above in the following:

The dotted line cell in this diagram corresponds to cell I of the above stated 2x2x2 design and is for treatment A, level I of the control variable 1, and levelIi of the control variable 2. From this design, it is possible to determine the main effects for three variables i.e., one experimental and true control variables. The researcher can also determine the interaction between each possible pair of variables (such interactions are called ‘first order interactions’) and interaction between variable taken in triplets (such interactions are called second order interactions). In case of a 2x2x2 design, the further given first order interactions are possible:
Experimental
variable with control variable 1 | (or EV
x CV 1); |
Experimental
variable with control variable 2 | (or EV
x CV 2); |
Control
variable 1 with control variable 2 | (or CV
1 x CV 2); |
There will be one second order interaction as well in the given design (it is between all the three variables i.e., EV x CV 1 x CV 2).
To determine the main effect for the experimental variable, the researcher must necessarily compare the combined mean of data in cells 1, 2, 3 and 4 for Treatment A with the combined mean of data in cells 5,6,7 and 8 for Treatment B. In this way the main effect of experimental variable, independent of control variable 1 and variable 2, is obtained. Similarly, the main effect for control variable 1, independent experimental variable and control variable 2, is obtained if we compare the combined mean of data in cells 1, 3, 5 and 7 with the combined mean of data in cells 2, 4, 6 and 8 of our 2x2x2 factorial design. On similar lines, one can determine the effect of control variable 2 independent of experimental variable and control variable 1, if the combined mean of data in cells 1,2,5 and 6 are compared with the combined mean of data in cells 3,4,7 and 8.
To obtain the first order interaction, say, for EV x CV 1 in the above stated design, the researcher must necessarily ignore control variable 2 for which purpose he may develop 2x2 design from the 2x2x2 design by combining the data of the relevant cells of the latter design as has been shown on next page:

Similarly, the researcher can determine other first order interactions. The analysis of the first order interaction in the manner described above is essentially a simple factorial analysis as only two variables are considered at a time and the remaining ones are ignored. But the analysis of the second order interaction would not ignore one of the three independent variables in case of a 2x2x2 design. The analysis would be termed as a complex factorial analysis.
It may, however, be remembered that the complex factorial design need not necessarily be of 2x2x2 type design, but can be generalized to any number and combinations of experimental and control independent variables. Of course, the greater the number of independent variables included in a complex factorial design, the higher the order of the interaction analysis possible. But the overall task goes on becoming more and more complicated with the inclusion of more and more independent variables in our design.
Factorial designs are used mainly because of the two advantages -
(i) They provide equivalent accuracy (as happens in the case of experiments with only one factor) with less labour and as such are source of economy. Using factorial designs, we can determine the effects of two (in simple factorial design) or more (in case of complex factorial design) factors (or variables) in one single experiment. (ii) they permit various other comparisons of interest. For example, they give information about such effects which cannot be obtained by treating one single factor at a time. The determination of interaction effects is possible in case of factorial designs.
Tags : Research Methodology - Experiments
Last 30 days 7068 views












