Research Methodology - Questionnaire & Sampling
Testing of hypothesis - Questionnaire & Sampling
Posted On :
As a part of investigation, samples are drawn from the population and results are derived to help in taking the decisions.
Testing
of hypothesis:
As a part of investigation, samples are drawn from the population and results are derived to help in taking the decisions. But such decisions involve an element of uncertainty causing wrong decisions. Hypothesis is an assumption which may or may not be true about a population parameter. For example, if we toss a coin 200 times, we may get 110 heads and 90 tails. At this instance, we are interested in testing whether the coin is unbiased or not.
Therefore, we may conduct a test to judge the significance of the difference of sampling or otherwise. To carry out a test of significance, the following procedure has to be followed:
To verify the assumption, which is based on sample study, we collect data and find out the difference between the sample value and the population value. If there is no difference found or the difference is very small then the hypothetical value is correct. Generally two hypotheses complementary to each offer are constructed, and if one is found correct, the other is rejected.
The random selection of the samples from the given population makes the tests of significance valid for us. For applying any test of significance we first set up a hypothesis- a definite statement about the population parameter/s. Such a statistical hypothesis, which is under test, is usually a hypothesis of no difference and hence is called null hypothesis. It is usually denoted by Ho. In the words of Prof. R.A.Fisher “Null Hypothesis is the hypothesis which is tested for possible rejection under the assumption that it is true.”
Any hypothesis which is complementary to the null hypothesis is called an alternative hypothesis. It is usually denoted by H1. It is very important to explicitly state the alternative hypothesis in respect of any null hypothesis H0 because the acceptance or rejection of Ho is meaningful only if it is being tested against an opposite hypothesis. For example, if we want to test the null hypothesis that the population has a specified mean µ0(say), i.e., H0:µ=µ then the alternative hypothesis could be:
Thus, in testing of hypothesis we are likely to commit two types of errors. The error of rejecting Ho when Ho is true is known as Type I Error and the error of accepting Ho when Ho is false is known as Type II Error.
As a part of investigation, samples are drawn from the population and results are derived to help in taking the decisions. But such decisions involve an element of uncertainty causing wrong decisions. Hypothesis is an assumption which may or may not be true about a population parameter. For example, if we toss a coin 200 times, we may get 110 heads and 90 tails. At this instance, we are interested in testing whether the coin is unbiased or not.
Therefore, we may conduct a test to judge the significance of the difference of sampling or otherwise. To carry out a test of significance, the following procedure has to be followed:
1. Framing the Hypothesis:
To verify the assumption, which is based on sample study, we collect data and find out the difference between the sample value and the population value. If there is no difference found or the difference is very small then the hypothetical value is correct. Generally two hypotheses complementary to each offer are constructed, and if one is found correct, the other is rejected.
(a) Null Hypothesis:
The random selection of the samples from the given population makes the tests of significance valid for us. For applying any test of significance we first set up a hypothesis- a definite statement about the population parameter/s. Such a statistical hypothesis, which is under test, is usually a hypothesis of no difference and hence is called null hypothesis. It is usually denoted by Ho. In the words of Prof. R.A.Fisher “Null Hypothesis is the hypothesis which is tested for possible rejection under the assumption that it is true.”
(b) Alternative Hypothesis.
Any hypothesis which is complementary to the null hypothesis is called an alternative hypothesis. It is usually denoted by H1. It is very important to explicitly state the alternative hypothesis in respect of any null hypothesis H0 because the acceptance or rejection of Ho is meaningful only if it is being tested against an opposite hypothesis. For example, if we want to test the null hypothesis that the population has a specified mean µ0(say), i.e., H0:µ=µ then the alternative hypothesis could be:
(i) H1:µ≠µ0 (i.e., µ>µ0 or µ<µ0)
(ii) H1: µ>µ0 (iii) H1: µ<µ0
The alternative hypothesis (i) is known as a two-tailed alternative and the alternatives in (ii) and (iii) are known as right-tailed and left-tailed alternatives. Accordingly, the corresponding tests of significance are called two-tailed, right-tailed and left-tailed tests respectively.
The null hypothesis consists of only a single parameter value and is usually simple while alternative hypothesis is usually composite.
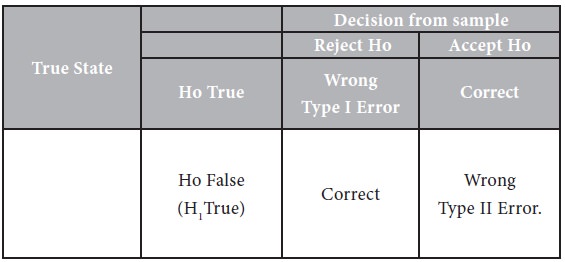
As stated earlier, the inductive inference consists in arriving at a decision to accept or reject a null hypothesis (Ho) after inspecting only a sample from it. As such an element of risk – the risk of taking wrong decision is involved. In any test procedure, the four possible mutually disjoint and exhaustive decisions are:
1. Reject Ho when actually it is not true i.e., when Ho is false.
2. Accept Ho when it is true.
3. Reject Ho when it is true.
4. Accept Ho when it is false.
The decisions in (i) and (ii) are correct decisions while the decisions in (iii) and (iv) are wrong decisions. These decisions may be expressed in the following dichotomous table:
The alternative hypothesis (i) is known as a two-tailed alternative and the alternatives in (ii) and (iii) are known as right-tailed and left-tailed alternatives. Accordingly, the corresponding tests of significance are called two-tailed, right-tailed and left-tailed tests respectively.
The null hypothesis consists of only a single parameter value and is usually simple while alternative hypothesis is usually composite.
Types Of Errors In Testing Of Hypothesis:
As stated earlier, the inductive inference consists in arriving at a decision to accept or reject a null hypothesis (Ho) after inspecting only a sample from it. As such an element of risk – the risk of taking wrong decision is involved. In any test procedure, the four possible mutually disjoint and exhaustive decisions are:
1. Reject Ho when actually it is not true i.e., when Ho is false.
2. Accept Ho when it is true.
3. Reject Ho when it is true.
4. Accept Ho when it is false.
The decisions in (i) and (ii) are correct decisions while the decisions in (iii) and (iv) are wrong decisions. These decisions may be expressed in the following dichotomous table:

Thus, in testing of hypothesis we are likely to commit two types of errors. The error of rejecting Ho when Ho is true is known as Type I Error and the error of accepting Ho when Ho is false is known as Type II Error.
For example, in the Industrial Quality Control, while
inspecting the quality of a manufactured lot, the Inspector commits Type I
Error when he rejects a good lot and he commits Type II Error when he accepts a
bad lot.
Tags : Research Methodology - Questionnaire & Sampling
Last 30 days 810 views












