Operations Management - Game Theory, Goal Programming & Queuing Theory
The Principle Of Dominance
Posted On :
In the previous lesson, we have discussed the method of solution of a game without a saddle point.
The Principle Of Dominance
In the previous lesson, we have discussed the method of solution of a game without a saddle point. While solving a game without a saddle point, one comes across the phenomenon of the dominance of a row over another row or a column over another column in the pay-off matrix of the game. Such a situation is discussed in the sequel.
In a given pay-off matrix A, we say that the ith row dominates the kth row if
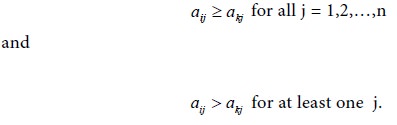
In such a situation player A will
never use the strategy corresponding to kth row, because he will gain less for
choosing such a strategy.
Similarly, we say the pth column
in the matrix dominates the qth column if
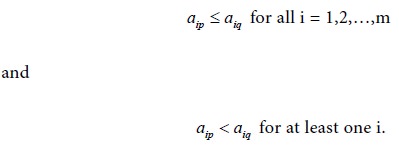
In this case, the player B will loose more by choosing the strategy for the qth column than by choosing the strategy for the pth column. So he will never use the strategy corresponding to the qth column. When dominance of a row ( or a column) in the pay-off matrix occurs, we can delete a row (or a column) from that matrix and arrive at a reduced matrix. This principle of dominance can be used in the determination of the solution for a given game.
Let us consider an illustrative example involving the phenomenon of dominance in a game.

The following condition holds:
Max {row minima} ≠ min {column maxima}
Therefore we see that there is no saddle point for the game under consideration.
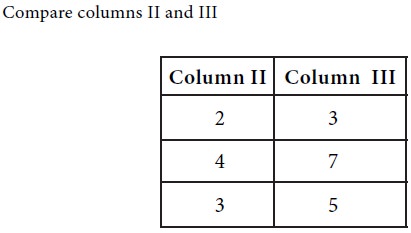
We see that each element in column III is greater than the corresponding element in column II. The choice is for player B. Since column II dominates column III, player B will discard his strategy 3.
Now we have the reduced game

For this matrix again, there is no saddle point. Column II dominates column IV. The choice is for player B. So player B will give up his strategy 4
The game reduces to the following:
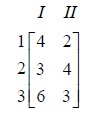
This matrix has no saddle point.
The third row dominates the first row. The choice is for player A. He will give up his strategy 1 and retain strategy 3. The game reduces to the following:
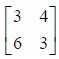
Again, there is no saddle point.
We have a 2x2 matrix. Take this matrix as
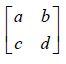
In the previous lesson, we have discussed the method of solution of a game without a saddle point. While solving a game without a saddle point, one comes across the phenomenon of the dominance of a row over another row or a column over another column in the pay-off matrix of the game. Such a situation is discussed in the sequel.
In a given pay-off matrix A, we say that the ith row dominates the kth row if
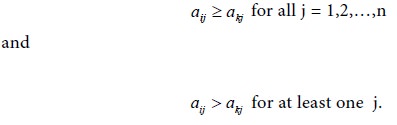
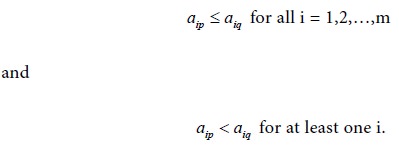
In this case, the player B will loose more by choosing the strategy for the qth column than by choosing the strategy for the pth column. So he will never use the strategy corresponding to the qth column. When dominance of a row ( or a column) in the pay-off matrix occurs, we can delete a row (or a column) from that matrix and arrive at a reduced matrix. This principle of dominance can be used in the determination of the solution for a given game.
Let us consider an illustrative example involving the phenomenon of dominance in a game.
Problem 1
Solve the game with the following pay-off matrix

Solve the game with the following pay-off matrix

Solution
First consider the minimum of each row.
First consider the minimum of each row.

The following condition holds:
Max {row minima} ≠ min {column maxima}
Therefore we see that there is no saddle point for the game under consideration.

We see that each element in column III is greater than the corresponding element in column II. The choice is for player B. Since column II dominates column III, player B will discard his strategy 3.
Now we have the reduced game

For this matrix again, there is no saddle point. Column II dominates column IV. The choice is for player B. So player B will give up his strategy 4
The game reduces to the following:
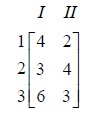
This matrix has no saddle point.
The third row dominates the first row. The choice is for player A. He will give up his strategy 1 and retain strategy 3. The game reduces to the following:
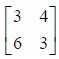
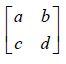
Then we have a = 3, b = 4, c = 6 and d = 3. Use the formulae for p, 1-p, r, 1-r and V.
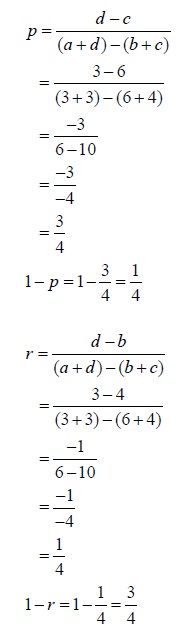
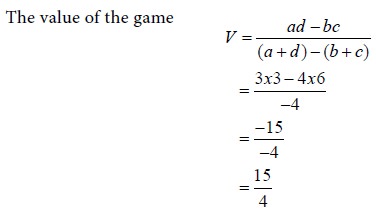
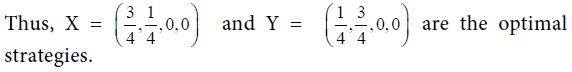
Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 1953 views












