Home | ARTS | Operations Management
|
Method of solution of a 2x2 zero-sum game without saddle point - Games With No Saddle Point
Operations Management - Game Theory, Goal Programming & Queuing Theory
Method of solution of a 2x2 zero-sum game without saddle point - Games With No Saddle Point
Posted On :
Suppose that a 2x2 game has no saddle point. Suppose the game has the following pay-off matrix.
Method
of solution of a 2x2 zero-sum game without saddle point
Suppose that a 2x2 game has no saddle point. Suppose the game has the following pay-off matrix.
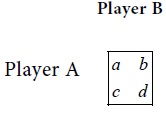
Since this game has no saddle
point, the following condition shall hold:
Max {Min {a , b}, Min {c , d }} ≠ Min {Max {a , c}, Max {b, d}}
In this case, the game is called a mixed game. No strategy of Player A can be called the best strategy for him. Therefore A has to use both of his strategies. Similarly no strategy of Player B can be called the best strategy for him and he has to use both of his strategies.
Let p be the probability that Player A will use his first strategy. Then the probability that Player A will use his second strategy is 1-p.
If Player B follows his first strategy
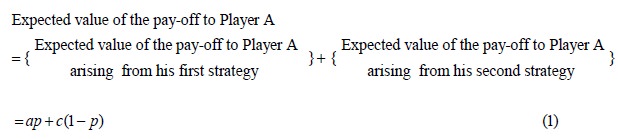
In the above equation, note that the expected value is got as the product of the corresponding values of the pay-off and the probability.
If Player B follows his second strategy
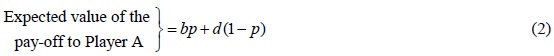
If the expected values in equations (1) and (2) are different, Player B will prefer the minimum of the two expected values that he has to give to player A. Thus B will have a pure strategy. This contradicts our assumption that the game is a mixed one. Therefore the expected values of the pay-offs to Player A in equations (1) and (2) should be equal. Thus we have the condition

To find the number of times that
B will use his first strategy and second strategy:
Let the probability that B will use his first strategy be r. Then the probability that B will use his second strategy is 1-r.
When A use his first strategy
The expected value of loss to Player B with his first strategy = ar
The expected value of loss to Player B with his second strategy = b(1-r)
When A use his second strategy
The expected value of loss to Player B with his first strategy = cr
The expected value of loss to Player B with his second strategy = d(1-r)
If the two expected values are
different then it results in a pure game, which is a contradiction. Therefore
the expected values of loss to Player B in equations (3) and (4) should be
equal. Hence we have the condition
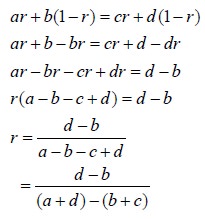
Problem 2
Solve the following game
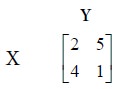
Solution
First consider the row minima.
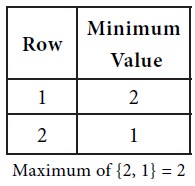
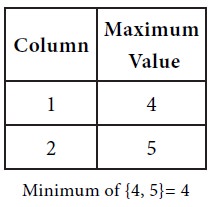
Next consider the maximum of each column


Therefore, out of 2 trials, player X will use his first strategy once and his second strategy once.
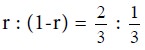
Therefore, out of 3 trials, player Y will use his first strategy twice and his second strategy once.
Suppose that a 2x2 game has no saddle point. Suppose the game has the following pay-off matrix.

Max {Min {a , b}, Min {c , d }} ≠ Min {Max {a , c}, Max {b, d}}
In this case, the game is called a mixed game. No strategy of Player A can be called the best strategy for him. Therefore A has to use both of his strategies. Similarly no strategy of Player B can be called the best strategy for him and he has to use both of his strategies.
Let p be the probability that Player A will use his first strategy. Then the probability that Player A will use his second strategy is 1-p.
If Player B follows his first strategy
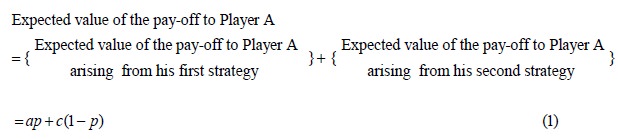
In the above equation, note that the expected value is got as the product of the corresponding values of the pay-off and the probability.
If Player B follows his second strategy
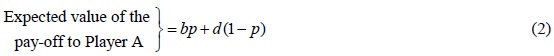
If the expected values in equations (1) and (2) are different, Player B will prefer the minimum of the two expected values that he has to give to player A. Thus B will have a pure strategy. This contradicts our assumption that the game is a mixed one. Therefore the expected values of the pay-offs to Player A in equations (1) and (2) should be equal. Thus we have the condition

Let the probability that B will use his first strategy be r. Then the probability that B will use his second strategy is 1-r.
When A use his first strategy
The expected value of loss to Player B with his first strategy = ar
The expected value of loss to Player B with his second strategy = b(1-r)
Therefore
the expected value of loss to B = ar + b(1-r) | (3) |
When A use his second strategy
The expected value of loss to Player B with his first strategy = cr
The expected value of loss to Player B with his second strategy = d(1-r)
Therefore
the expected value of loss to B = cr + d(1-r) | (4) |
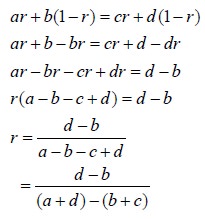
Solve the following game
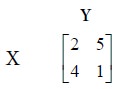
Solution
First consider the row minima.

Next consider the maximum of each column



Therefore, out of 2 trials, player X will use his first strategy once and his second strategy once.
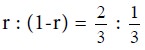
Therefore, out of 3 trials, player Y will use his first strategy twice and his second strategy once.
Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 4005 views












