Operations Management - Game Theory, Goal Programming & Queuing Theory
Assumptions for two-person zero sum game
Posted On :
For building any model, certain reasonable assumptions are quite necessary.
Assumptions
for two-person zero sum game
For building any model, certain reasonable assumptions are quite necessary. Some assumptions for building a model of two-person zero sum game are listed below.
a. Each player has available to him a finite number of possible courses of action. Sometimes the set of courses of action may be the same for each player. Or, certain courses of action may be available to both players while each player may have certain specific courses of action which are not available to the other player.
b. Player A attempts to maximize gains to himself. Player B tries to minimize losses to himself.
c. The decisions of both players are made individually prior to the play with no communication between them.
d. The decisions are made and announced simultaneously so that neither player has an advantage resulting from direct knowledge of the other player’s decision.
e. Both players know the possible payoffs of themselves and their opponents.
The selection of an optimal strategy by each player without the knowledge of the competitor’s strategy is the basic problem of playing games.
The objective of game theory is to know how these players must select their respective strategies, so that they may optimize their payoffs. Such a criterion of decision making is referred to as minimax-maximin principle. This principle in games of pure strategies leads to the best possible selection of a strategy for both players.
For example, if player A chooses his ith strategy, then he gains at least the payoff min aij , which is minimum of the ith row elements in the payoff matrix. Since his objective is to maximize his payoff, he can choose strategy i so as to make his payoff as large as possible. i.e., a payoff which is not less than max min aij .
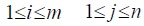
Similarly player B can choose jth column elements so as to make his loss
not greater than max min aij .
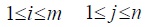
If the maximin value for a player is equal to the
minimax value for another player, i.e.
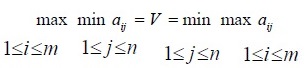
then the game is said to have a saddle point
(equilibrium point) and the corresponding strategies are called optimal
strategies. If there are two or more saddle points, they must be equal.
The amount of payoff, i.e., V at an equilibrium point is known as the value of the game.
The optimal strategies can be identified by the players in the long run.
The game is said to be fair if the value of the game V = 0.
For building any model, certain reasonable assumptions are quite necessary. Some assumptions for building a model of two-person zero sum game are listed below.
a. Each player has available to him a finite number of possible courses of action. Sometimes the set of courses of action may be the same for each player. Or, certain courses of action may be available to both players while each player may have certain specific courses of action which are not available to the other player.
b. Player A attempts to maximize gains to himself. Player B tries to minimize losses to himself.
c. The decisions of both players are made individually prior to the play with no communication between them.
d. The decisions are made and announced simultaneously so that neither player has an advantage resulting from direct knowledge of the other player’s decision.
e. Both players know the possible payoffs of themselves and their opponents.
Minimax and Maximin Principles
The selection of an optimal strategy by each player without the knowledge of the competitor’s strategy is the basic problem of playing games.
The objective of game theory is to know how these players must select their respective strategies, so that they may optimize their payoffs. Such a criterion of decision making is referred to as minimax-maximin principle. This principle in games of pure strategies leads to the best possible selection of a strategy for both players.
For example, if player A chooses his ith strategy, then he gains at least the payoff min aij , which is minimum of the ith row elements in the payoff matrix. Since his objective is to maximize his payoff, he can choose strategy i so as to make his payoff as large as possible. i.e., a payoff which is not less than max min aij .
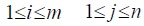
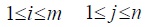
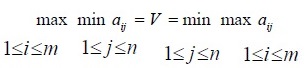
The amount of payoff, i.e., V at an equilibrium point is known as the value of the game.
The optimal strategies can be identified by the players in the long run.
Fair game
The game is said to be fair if the value of the game V = 0.
Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 1862 views












