Home | ARTS | Operations Management
|
Method of convex linear combination - The Principle Of Dominance
Operations Management - Game Theory, Goal Programming & Queuing Theory
Method of convex linear combination - The Principle Of Dominance
Posted On :
A strategy, say s, can also be dominated if it is inferior to a convex linear combination of several other pure strategies.
Method
of convex linear combination
A strategy, say s, can also be dominated if it is inferior to a convex linear combination of several other pure strategies. In this case if the domination is strict, then the strategy s can be deleted. If strategy s dominates the convex linear combination of some other pure strategies, then one of the pure strategies involved in the combination may be deleted. The domination will be decided as per the above rules. Let us consider an example to illustrate this case.
Problem 2
Solve the game with the following pay-off matrix for firm A

Solution
First consider the minimum of each row
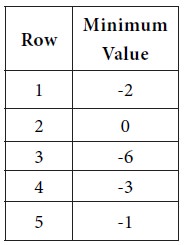
Maximum of {-2, 0, -6, -3, -1} = 0
Next consider the maximum of each column.
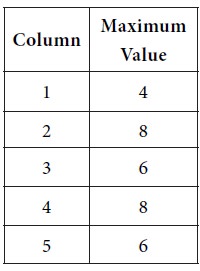
Minimum of { 4, 8, 6, 8, 6}= 4
Hence,
Maximum of {row minima} ≠ minimum of {column maxima}
So we see that there is no saddle point. Compare the second row with the fifth row. Each element in the second row exceeds the corresponding element in the fifth row. Therefore, A2 dominates A5 . The choice is for firm A. It will retain strategy A2 and give up strategy A5 . Therefore the game reduces to the following.

Compare the second and fourth rows. We see that A2 dominates A4 . So, firm A will retain the
strategy A2 and give up the strategy A4 . Thus the game reduces to the following:

Compare the first and fifth columns. It is observed
that B1 dominates B5. The choice is for firm B. It will retain the strategy B1 and give up the strategy B5 . Thus the game reduces to the
following
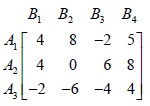
Compare the first and fourth columns. We notice
that B1 dominates B4. So firm B will discard the strategy B4 and retain the strategy B1 . Thus the game reduces to the
following:
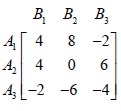
For this
reduced game, we check that there is no saddle point.
Now none of the pure strategies of firms A and B is inferior to any of their other strategies. But, we observe that convex linear combination of the strategies B2 and B3 dominates B1 , i.e. the averages of payoffs due to strategies B2 and B3 ,
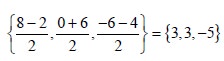
dominate B1 . Thus B1 may be omitted from consideration. So we have the reduced matrix
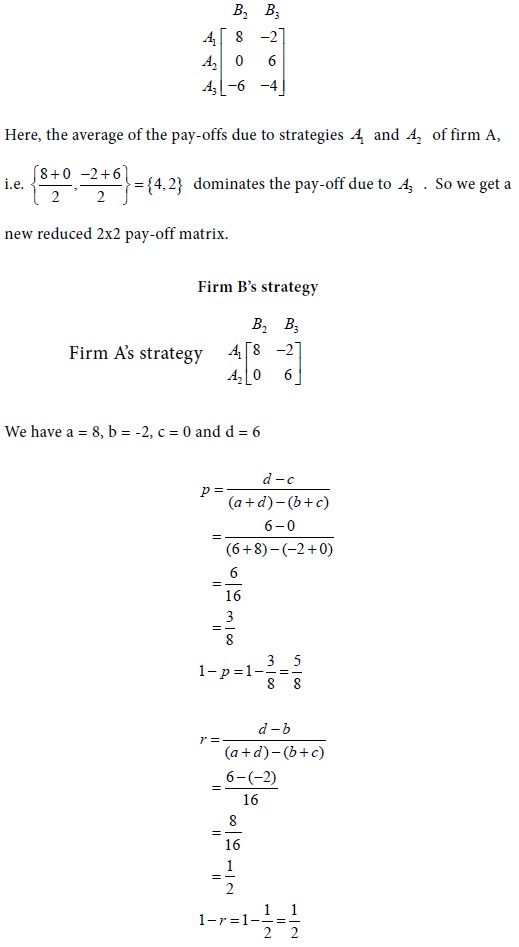
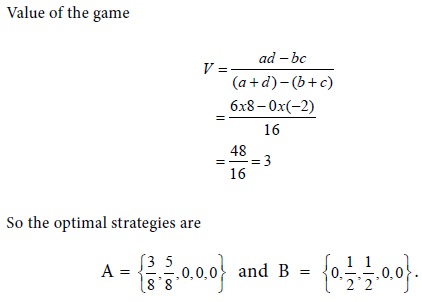
The value of the game = 3. Thus the game is favourable to firm A.
Problem 3
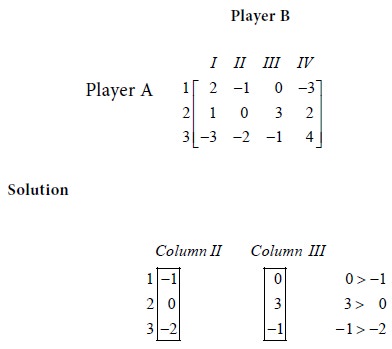
For the game with the following pay-off matrix, determine the saddle point
The
choice is with the player B. He has to choose between strategies II and III. He will lose more in strategy III than in strategy II,
irrespective of what strategy is followed by A. So he will drop strategy III
and retain

Maximum of row minimum = Minimum of column maximum = 0.
So, a saddle point exists for the given game and the value of the game is 0.
Interpretation
No player gains and no player loses. i.e., The game is not favourable to any player. i.e. It is a fair game.

Since Maximum of { Row Minima} and Minimum of { Column Maxima } are
different, it follows that the given game has no saddle point.
Denote the strategies of player A by A1 , A2 , A3 . Denote the strategies of
player B by B1 , B2 , B3 . Compare the first and third
columns of the given matrix.
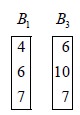
The pay-offs in B3 are greater than or equal to the corresponding pay-offs in B1 . The player B has to make a choice between his strategies 1 and 3. He will lose more if he follows strategy 3 rather than strategy 1. Therefore he will give up strategy 3 and retain strategy 1. Consequently, the given game is transformed into the following game
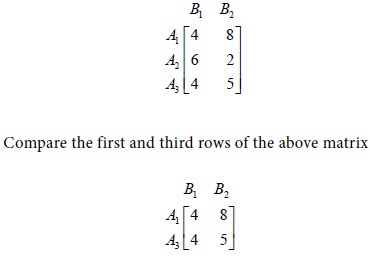
The pay-offs in A1 are greater than or equal to the corresponding pay-offs in A3 . The player A has to make a choice between his strategies 1 and 3. He
will gain more if he follows strategy 1 rather than strategy 3. Therefore he
will retain strategy 1 and give up strategy 3. Now the given game is
transformed into the following game.
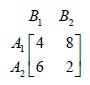

Maximum {row minima} and Minimum {column maxima }
are not equal Therefore, the reduced game has no saddle point. So, it is a
mixed game

The probability that player A will use his first strategy is p. This is
calculated as
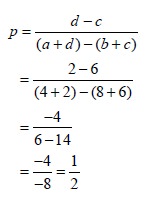
The probability that player B will use his first strategy is r. This is calculated as
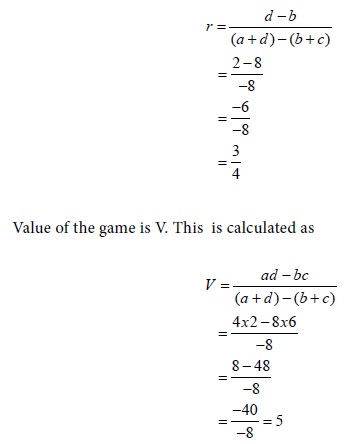
Interpretation


We see that Maximum of { row minima} ≠ Minimum of { column maxima}.
We assert that Player B will retain the first strategy and give up the third strategy. We get the following reduced matrix.
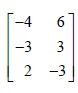
We check that it is a game with no saddle point.
Sub games
Let us consider the 2x2 sub games. They are:


A strategy, say s, can also be dominated if it is inferior to a convex linear combination of several other pure strategies. In this case if the domination is strict, then the strategy s can be deleted. If strategy s dominates the convex linear combination of some other pure strategies, then one of the pure strategies involved in the combination may be deleted. The domination will be decided as per the above rules. Let us consider an example to illustrate this case.
Problem 2
Solve the game with the following pay-off matrix for firm A

Solution
First consider the minimum of each row

Maximum of {-2, 0, -6, -3, -1} = 0
Next consider the maximum of each column.

Minimum of { 4, 8, 6, 8, 6}= 4
Hence,
Maximum of {row minima} ≠ minimum of {column maxima}
So we see that there is no saddle point. Compare the second row with the fifth row. Each element in the second row exceeds the corresponding element in the fifth row. Therefore, A2 dominates A5 . The choice is for firm A. It will retain strategy A2 and give up strategy A5 . Therefore the game reduces to the following.


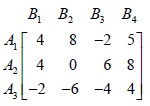
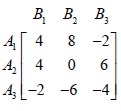
Now none of the pure strategies of firms A and B is inferior to any of their other strategies. But, we observe that convex linear combination of the strategies B2 and B3 dominates B1 , i.e. the averages of payoffs due to strategies B2 and B3 ,
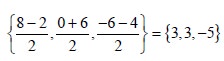
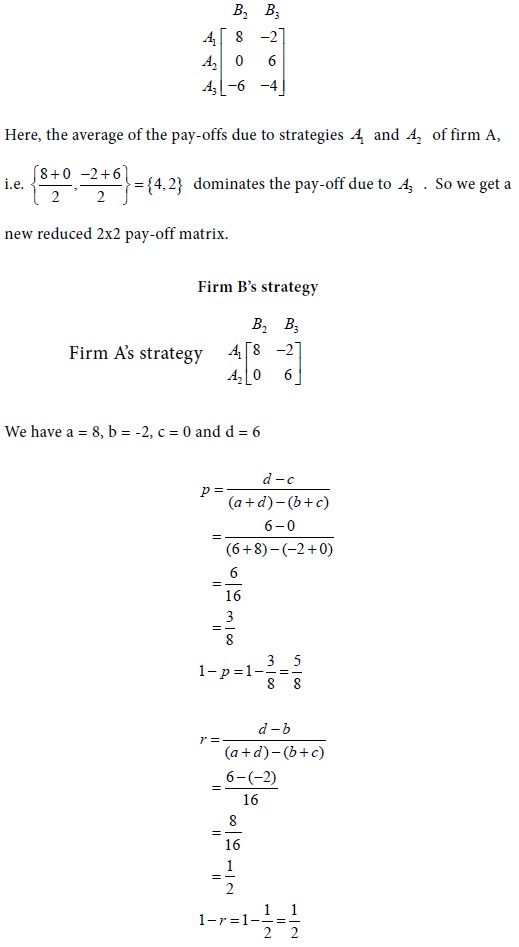
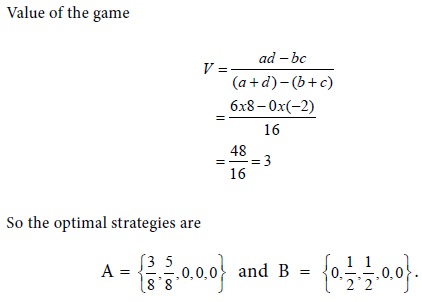
The value of the game = 3. Thus the game is favourable to firm A.
Problem 3
For the game with the following pay-off matrix, determine the saddle point


Maximum of row minimum = Minimum of column maximum = 0.
So, a saddle point exists for the given game and the value of the game is 0.
Interpretation
No player gains and no player loses. i.e., The game is not favourable to any player. i.e. It is a fair game.


The pay-offs in B3 are greater than or equal to the corresponding pay-offs in B1 . The player B has to make a choice between his strategies 1 and 3. He will lose more if he follows strategy 3 rather than strategy 1. Therefore he will give up strategy 3 and retain strategy 1. Consequently, the given game is transformed into the following game
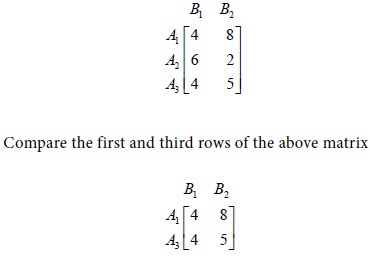
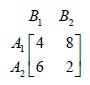


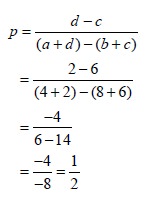
The probability that player B will use his first strategy is r. This is calculated as
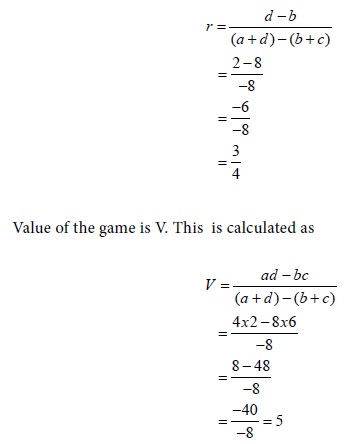
Interpretation
Out of 3 trials, player A will
use strategy 1 once and strategy 2 once. Out of 4 trials, player B will use
strategy 1 thrice and strategy 2 once. The game is favourable to player A.
Problem 5
Dividing a game into sub-games
Solve the game with the following pay-off matrix.
Problem 5
Dividing a game into sub-games
Solve the game with the following pay-off matrix.


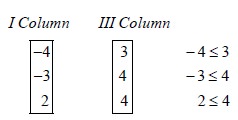
We see that Maximum of { row minima} ≠ Minimum of { column maxima}.
So the game has no saddle point. Hence it
is a mixed game. Compare the first and third columns

We assert that Player B will retain the first strategy and give up the third strategy. We get the following reduced matrix.
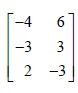
We check that it is a game with no saddle point.
Sub games
Let us consider the 2x2 sub games. They are:


The value of 0 will be preferred
by the player A. For this value, the first and third strategies of A correspond
while the first and second strategies of the player B correspond to the value 0
of the game. So it is a fair game.
Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 1993 views












