Home | ARTS | Operations Management
|
Model 4 - Determining Economic Order Quantities-Deterministic Models – Purchase Order Quantities without shortages
Operations Management - Transportation / Assignment & Inventory Management
Model 4 - Determining Economic Order Quantities-Deterministic Models – Purchase Order Quantities without shortages
Posted On :
Finding the EOQ with shortages and the replenishment of inventory is at a finite rate
Model 4
Finding the EOQ with shortages and the replenishment of inventory is at a finite rate
An Illustration: Consider the example, which is given in the Model 1. Assume that you are requiring Rs. 100 per day and in a month your demand is Rs. 3000/- to manage your requirements. Again, you may get your required amount immediately. Only the change is, instead of giving your demand Rs. 3000/- in a single stroke, your parents decided to give the sum in such a way that first 20 days, you will be given with Rs. 150/-per day out of which Rs. 100/- per day is incurred and every day you have to save Rs. 50/- for the first twenty days, and you will not be given any amount after 20th. The remaining days in the month, you will start using
If we consider companies such as Hyundai, Maruti and other bigger automobiles, they use to follow this kind of ‘constant rate of replenishment’ instead of instantaneous replenishment. If a truck manufacturer who is placing an order of 10,000 Tyres would appreciate the concept of finite rate of fulfilling the orders rather than getting all the 10,000 Tyres in a single stroke. He may save a lot in keeping smaller warehouse(s), capital locked in inventory is minimal. For the supplier also, he finds it convenient to sending the quantities in batches rather than bulk dispatches. But all these relaxation have a binding such that the quantities should be supplied on specified date and time, any violation should dealt very severally by levying large penalties.
2.
Let ‘k’
be the rate of replenishment per unit of time.
3. Shortages are permitted and let C2 be the shortage cost per unit per unit of time.
4.
Lead-time
is zero.
5. Let C1 be the holding cost per unit of inventory per unit of time.
6. Let Cs be the set up cost per production run or ordering cost per cycle.
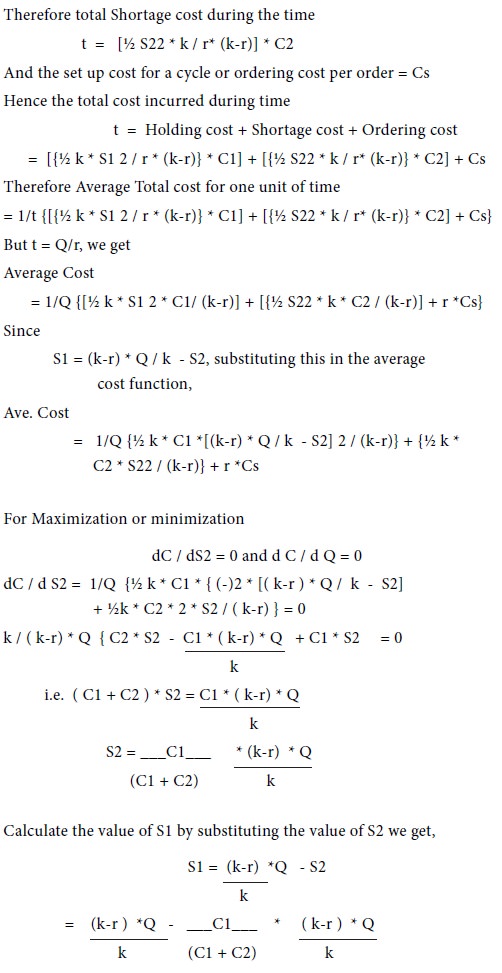

Example
The demand for an item in a company is 12000 per year and the company can produce the item at the rate of 3000 per month. The cost of one set up is Rs. 500 and the holding cost of one unit per month is Rs 0.15. The shortage cost of one unit is Rs. 20 per year. Determine the optimum manufacturing quantity and the # of production runs and time between the production runs?
Solution
The given quantities can be summarized in the following table.

Finding the EOQ with shortages and the replenishment of inventory is at a finite rate
An Illustration: Consider the example, which is given in the Model 1. Assume that you are requiring Rs. 100 per day and in a month your demand is Rs. 3000/- to manage your requirements. Again, you may get your required amount immediately. Only the change is, instead of giving your demand Rs. 3000/- in a single stroke, your parents decided to give the sum in such a way that first 20 days, you will be given with Rs. 150/-per day out of which Rs. 100/- per day is incurred and every day you have to save Rs. 50/- for the first twenty days, and you will not be given any amount after 20th. The remaining days in the month, you will start using
If we consider companies such as Hyundai, Maruti and other bigger automobiles, they use to follow this kind of ‘constant rate of replenishment’ instead of instantaneous replenishment. If a truck manufacturer who is placing an order of 10,000 Tyres would appreciate the concept of finite rate of fulfilling the orders rather than getting all the 10,000 Tyres in a single stroke. He may save a lot in keeping smaller warehouse(s), capital locked in inventory is minimal. For the supplier also, he finds it convenient to sending the quantities in batches rather than bulk dispatches. But all these relaxation have a binding such that the quantities should be supplied on specified date and time, any violation should dealt very severally by levying large penalties.
Solution
Let us have the following assumptions:
1. Demand is known and uniform. Let ‘r’ be the rate of demand for one unit of time.
Let us have the following assumptions:
1. Demand is known and uniform. Let ‘r’ be the rate of demand for one unit of time.
3. Shortages are permitted and let C2 be the shortage cost per unit per unit of time.
5. Let C1 be the holding cost per unit of inventory per unit of time.
6. Let Cs be the set up cost per production run or ordering cost per cycle.
Assume that each production run of length‘t’
consists of 2 parts say t1 and t2. In turn, they are sub divided into t11, t12
and t21, t22 as shown in the figure.


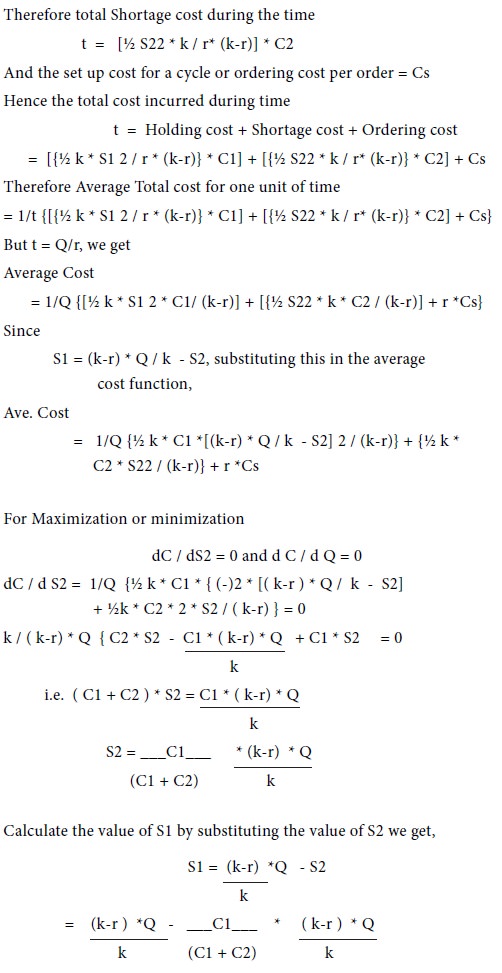

Example
The demand for an item in a company is 12000 per year and the company can produce the item at the rate of 3000 per month. The cost of one set up is Rs. 500 and the holding cost of one unit per month is Rs 0.15. The shortage cost of one unit is Rs. 20 per year. Determine the optimum manufacturing quantity and the # of production runs and time between the production runs?
Solution
The given quantities can be summarized in the following table.

Tags : Operations Management - Transportation / Assignment & Inventory Management
Last 30 days 676 views












