Home | ARTS | Operations Management
|
Model 3 - Determining Economic Order Quantities-Deterministic Models – Purchase Order Quantities without shortages
Operations Management - Transportation / Assignment & Inventory Management
Model 3 - Determining Economic Order Quantities-Deterministic Models – Purchase Order Quantities without shortages
Posted On :
E.B.Q with known demand, shortages is permitted and replenishment of inventory is instantaneous
Model – 3
E.B.Q with known demand, shortages is permitted and replenishment of inventory is instantaneous
Illustration: Consider the example, discussed in the Model – 1. Assume that you are required (as a student) Rs. 100/- to meet your daily requirements such as food, stay, refreshment etc. In a month, your demand is Rs. 3000/-. Whenever you are contacting parents, they are in a position to give your requirements in single stroke on the day itself. To get the money, you have to go to your native which costs you say Rs. 50/- Instead of keeping the money in your room, if you keep it in a bank, you may get an interest of Rs.20/- month. Every month, 25th assume your roommate used to get Rs. 500/- from you. Because of this practice, you find that you are running out cash on every 25th. However, you can borrow the amount from neighbor/friends at nominal interest rates. If this is the situation given to you, how much you have to get from your parents such that your holding/opportunity cost and ordering/ procurement cost is, get balanced?
Again, consider the example of a car manufacturer, whose requirement is say 3000 Gear boxes per month, who is producing 100 cars in a day, finds that keeping a gear box in warehouse costs him Rs. 200/- per month (of course, excluding cost of gear box) and placing the order would costs Rs. 500 per order. In addition to this, he included a
Solution
Let us have the following assumptions.
1. Demand is known and uniform. Let D be the total demand for one unit of time.
2. Shortages are permitted, and let C2 is the shortage cost per quantity per unit of time.
3. Production of the item or procurement is instantaneous.
4. Lead -time is zero.
5. Let C1 be the inventory holding cost per unit. Per unit of time
6. Let Cs be the set up or ordering cost for every production run (or cycle).
Divide the given total time period into ‘n’ units each of time‘t’


Example-1
Raja Motors, a contractor undertakes to supply diesel engines to a truck manufacturer at the rate of 25 engines per day. There is a class in the contract for penalizing him for missing the scheduled delivery date. Rs 1000/- per engine per day is the penalty charged on Raja Motors. He finds that the cost of holding a completed engine in stock is Rs. 120/- per month. His production process is such that he can produce enough engines within a short time. Determine how often he can make a production run, and what size it should be, if he has to incur Rs. 10000 every time, whenever a production run is made.
Solution
The given data can be summarized in the following table.

Example-2
The demand for soap is 50 units per month and the products are withdrawn uniformly. The expenses incurred while purchasing for each time is Rs. 200/-. The cost of each soap is Rs 20/- per item and the inventory holding cost of Rs. 4 per item per month. In addition, a profit of Rs 2 per item per month is gained from selling the soap. Determine how often to make purchases and what size it should be such that it will minimize the total inventory cost?
Solution
From the given problem, we identify the following information /costs; Demand for the item, D = 50/month
Holding cost C1, = Rs. 4/month
Shortage Cost C2, = Rs 2/month/per unit
Set up cost Cs, = Rs. 200
Substituting these values in the equation for EOQ, we get,

Example-3
The demand for Gem Clips is uniform at a rate of 200 boxes /month. The fixed cost Rs 10 is incurred each time while purchase is made. The cost of each box is Rs. 10 per item and the inventory carrying cost is Rs 0.25 per box per month. The shortages are penalized at the rate of Rs. 1.25 per box per month; determine what should be the purchase cycle what size it should be?
Solution
From the given problem, we identify the following information /
costs;
Demand, D = 200 boxes/month
Penalty Charges, C2 = 1.25/month/box
Purchasing cost, Cs = Rs. 10
Holding cost, C1 = 0.25/box/month
Substituting these values in the equation for EOQ, we get,

Example-4
SMS Electronics Ltd., which is manufacturing Color televisions also, produces its own speakers, which are used in television sets. Since the company produces 8 models of its color televisions with product codes as (TFR-CTV/01 to TFR-CTV/08). The television sets are assembled on a continuous production line at a rate of 8000 per month. The speakers are produced in batches because they do not warrant setting up a continuous production line and relatively large quantities can be produced in a short time. Discuss the problem of the company, determining when and how much to produce given the following data.
1. Each time a batch is produced, a set up cost of Rs. 12000/- is incurred, as the models are differing in technologies and appearances and component requirements.
2. The cost of keeping a quality checked speakers (QC-Passed Speakers) in stock is 30 paisa per day.
3. The production cost of a single speaker excluding the set up cost is Rs. 1000 and can be assumed a unit cost.
4. Shortage is going to stop the production and estimated that Rs. 1.10 month whenever a speaker is not available.
Solution
From the given problem, we identify the following information / costs;
Holding cost, C1 =9.90/month/unit
Shortage Cost, C2 = 1.10/month/unit
Substituting these values in the equation for EOQ, we get,

E.B.Q with known demand, shortages is permitted and replenishment of inventory is instantaneous
Illustration: Consider the example, discussed in the Model – 1. Assume that you are required (as a student) Rs. 100/- to meet your daily requirements such as food, stay, refreshment etc. In a month, your demand is Rs. 3000/-. Whenever you are contacting parents, they are in a position to give your requirements in single stroke on the day itself. To get the money, you have to go to your native which costs you say Rs. 50/- Instead of keeping the money in your room, if you keep it in a bank, you may get an interest of Rs.20/- month. Every month, 25th assume your roommate used to get Rs. 500/- from you. Because of this practice, you find that you are running out cash on every 25th. However, you can borrow the amount from neighbor/friends at nominal interest rates. If this is the situation given to you, how much you have to get from your parents such that your holding/opportunity cost and ordering/ procurement cost is, get balanced?
Again, consider the example of a car manufacturer, whose requirement is say 3000 Gear boxes per month, who is producing 100 cars in a day, finds that keeping a gear box in warehouse costs him Rs. 200/- per month (of course, excluding cost of gear box) and placing the order would costs Rs. 500 per order. In addition to this, he included a
Solution
Let us have the following assumptions.
1. Demand is known and uniform. Let D be the total demand for one unit of time.
4. Lead -time is zero.
5. Let C1 be the inventory holding cost per unit. Per unit of time
6. Let Cs be the set up or ordering cost for every production run (or cycle).
Divide the given total time period into ‘n’ units each of time‘t’
n * t = 1
Let Q be the EBQ for every run
The total demand D = n *Q
Let us assume that each production run consists of 2 parts say t1 and t2 such that during the interval t1 items are drawn from the inventory as needed and during t2, orders for the item are being accumulated, but not filled. And at the end of interval ‘ t ‘ an amount Q is ordered, the amount Q is divided into Q1 and Q2 such that Q1 + Q2 = Q where Q1 denotes the amount that goes into the inventory and Q2 denotes the amount that is immediately taken to satisfy unfilled demands.
The Graph of this model is given below.
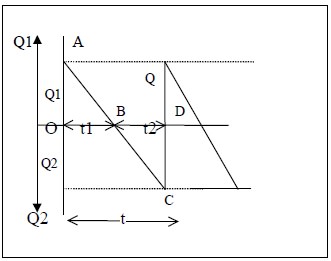
Let Q be the EBQ for every run
The total demand D = n *Q
Let us assume that each production run consists of 2 parts say t1 and t2 such that during the interval t1 items are drawn from the inventory as needed and during t2, orders for the item are being accumulated, but not filled. And at the end of interval ‘ t ‘ an amount Q is ordered, the amount Q is divided into Q1 and Q2 such that Q1 + Q2 = Q where Q1 denotes the amount that goes into the inventory and Q2 denotes the amount that is immediately taken to satisfy unfilled demands.
The Graph of this model is given below.



Example-1
Raja Motors, a contractor undertakes to supply diesel engines to a truck manufacturer at the rate of 25 engines per day. There is a class in the contract for penalizing him for missing the scheduled delivery date. Rs 1000/- per engine per day is the penalty charged on Raja Motors. He finds that the cost of holding a completed engine in stock is Rs. 120/- per month. His production process is such that he can produce enough engines within a short time. Determine how often he can make a production run, and what size it should be, if he has to incur Rs. 10000 every time, whenever a production run is made.
Solution
The given data can be summarized in the following table.

Example-2
The demand for soap is 50 units per month and the products are withdrawn uniformly. The expenses incurred while purchasing for each time is Rs. 200/-. The cost of each soap is Rs 20/- per item and the inventory holding cost of Rs. 4 per item per month. In addition, a profit of Rs 2 per item per month is gained from selling the soap. Determine how often to make purchases and what size it should be such that it will minimize the total inventory cost?
Solution
From the given problem, we identify the following information /costs; Demand for the item, D = 50/month
Holding cost C1, = Rs. 4/month
Shortage Cost C2, = Rs 2/month/per unit
Set up cost Cs, = Rs. 200
Substituting these values in the equation for EOQ, we get,

Example-3
The demand for Gem Clips is uniform at a rate of 200 boxes /month. The fixed cost Rs 10 is incurred each time while purchase is made. The cost of each box is Rs. 10 per item and the inventory carrying cost is Rs 0.25 per box per month. The shortages are penalized at the rate of Rs. 1.25 per box per month; determine what should be the purchase cycle what size it should be?
Solution
From the given problem, we identify the following information /
costs;
Demand, D = 200 boxes/month
Penalty Charges, C2 = 1.25/month/box
Purchasing cost, Cs = Rs. 10
Holding cost, C1 = 0.25/box/month
Substituting these values in the equation for EOQ, we get,

Example-4
SMS Electronics Ltd., which is manufacturing Color televisions also, produces its own speakers, which are used in television sets. Since the company produces 8 models of its color televisions with product codes as (TFR-CTV/01 to TFR-CTV/08). The television sets are assembled on a continuous production line at a rate of 8000 per month. The speakers are produced in batches because they do not warrant setting up a continuous production line and relatively large quantities can be produced in a short time. Discuss the problem of the company, determining when and how much to produce given the following data.
1. Each time a batch is produced, a set up cost of Rs. 12000/- is incurred, as the models are differing in technologies and appearances and component requirements.
Solution
From the given problem, we identify the following information / costs;
Demand, D = 8000 | |
Set up cost, Cs = | 12000 |
Shortage Cost, C2 = 1.10/month/unit
Substituting these values in the equation for EOQ, we get,

Tags : Operations Management - Transportation / Assignment & Inventory Management
Last 30 days 1005 views












