Operations Management - Network Problems
Determination of Project Completion Time in PERT
Posted On :
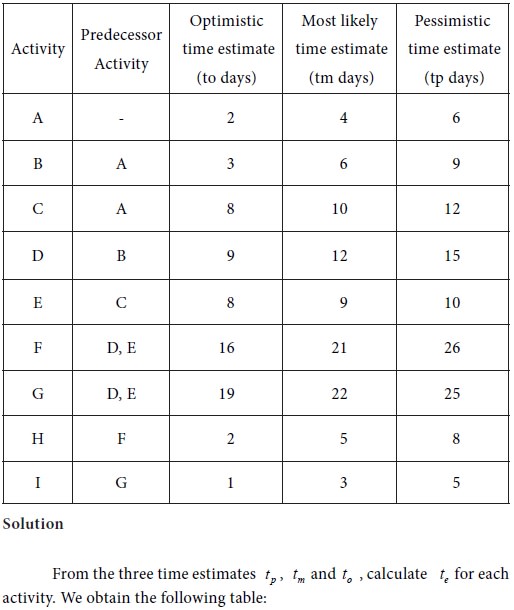
Find out the time required to complete the following project and the critical activities:
Determination of Project
Completion Time in PERT
Problem 2
Find out the time required to complete the following project and the critical activities:
Consider the paths, beginning with the start node
and stopping with the end node. There are four such paths for the given
project. They are as follows:
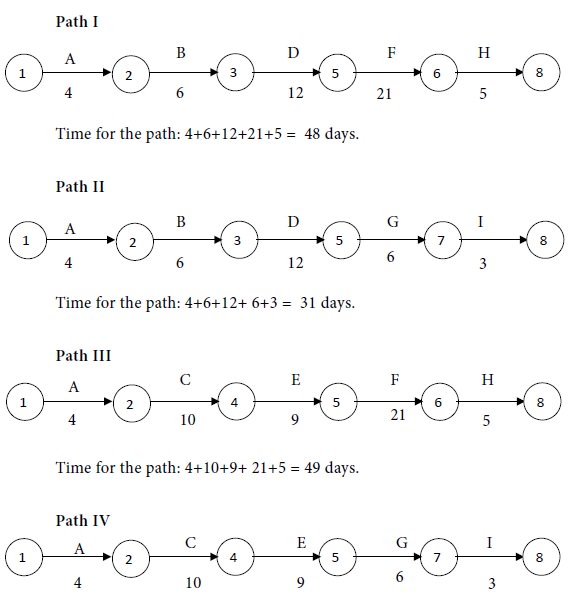
Time for the path: 4+10+9+ 6+3 = 32 days.
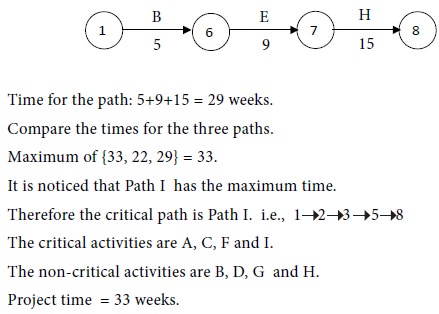
Compare the times for the four paths.
Maximum of {48, 31, 49, 32} = 49.
We see that Path III has the maximum time.
Therefore the critical path is Path III. i.e.,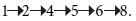

The critical activities are A, C, E, F and H.
The non-critical activities are B, D, G and I.
Project time (Also called project length) = 49 days.
Problem 3
Find out
the time, variance and standard deviation of the project with the following
time estimates in weeks:
Solution
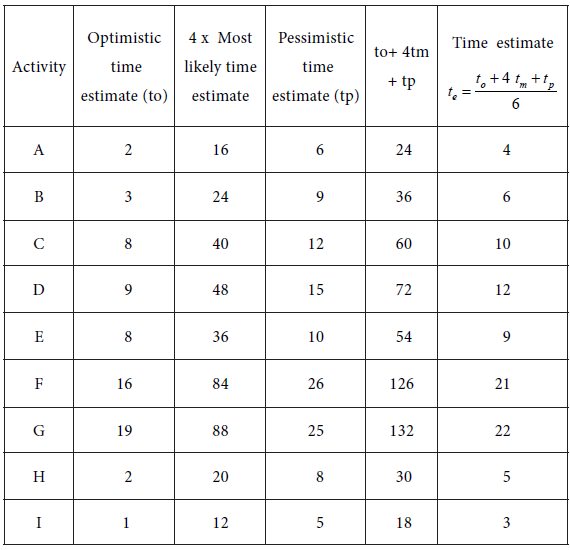
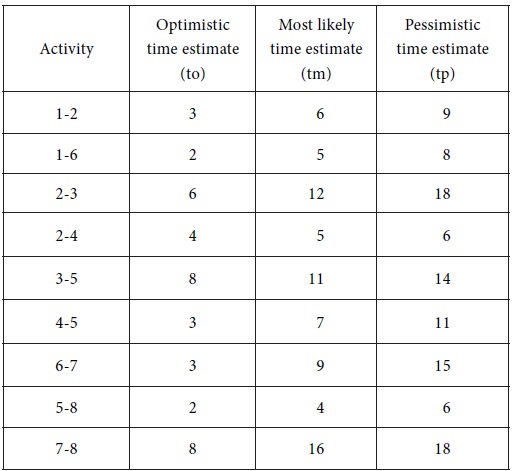
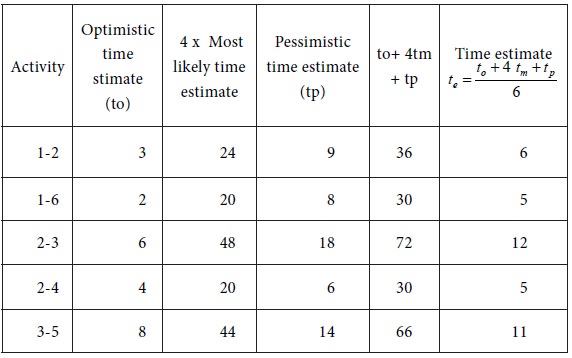
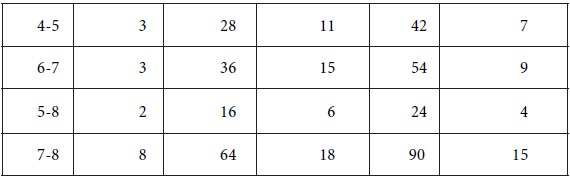
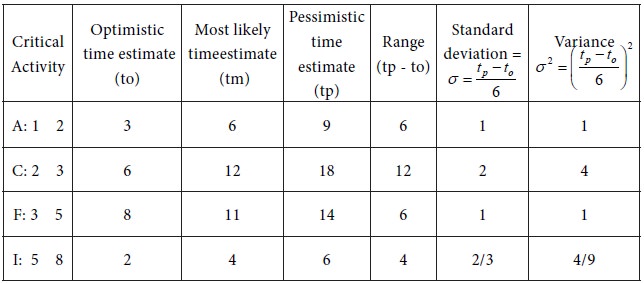
From the three time estimates tp , tm and to , calculate te for each activity. We obtain the following table:
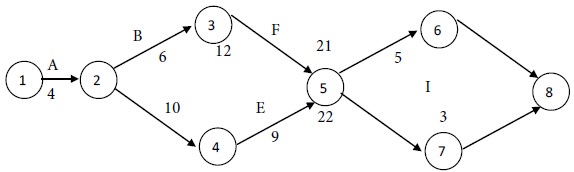
With the single time estimates of the activities, we get the following network diagram for the project.
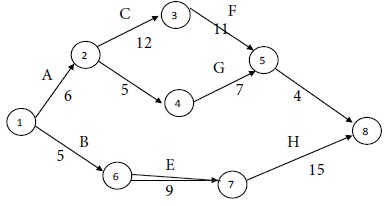
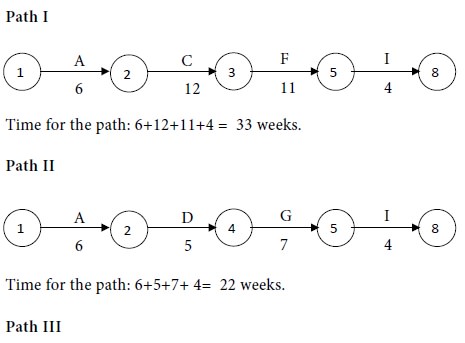
Consider the paths, beginning with the start node and stopping with the end node. There are three such paths for the given project. They are as follows:
Standard deviation of project time = √Variance =
√58/9 = 2.54 weeks.
Problem 4
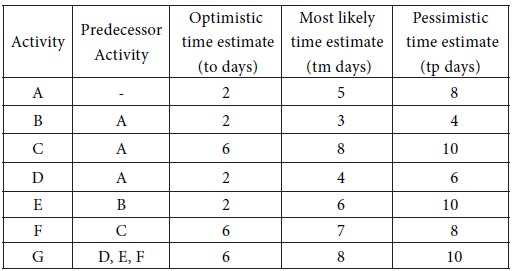
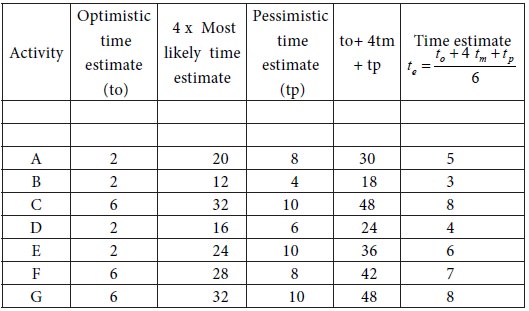
A project consists of seven activities with the following time estimates. Find the probability that the project will be completed in 30 weeks or less.
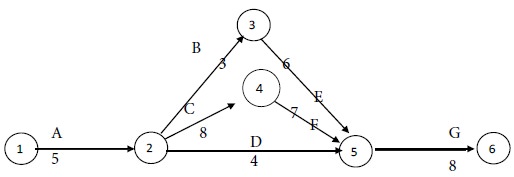
With the single time estimates of the activities, the following network diagram is constructed for the project.
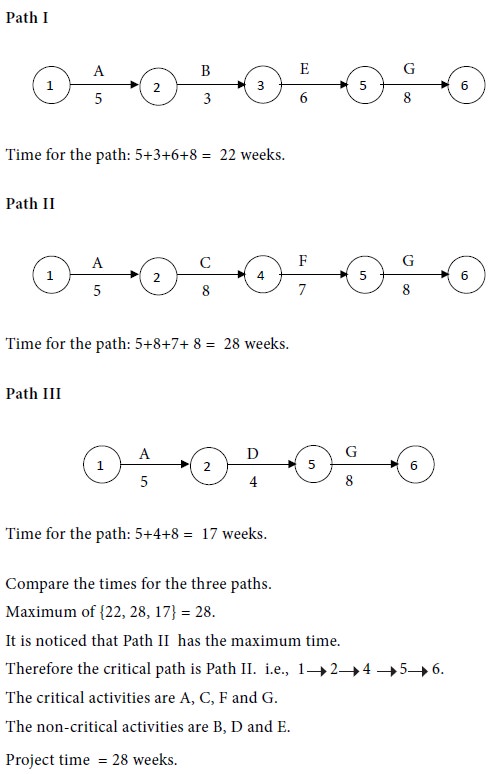
Consider the paths, beginning with the start node
and stopping with the end node. There are three such paths for the given
project. They are as follows:
We refer to the Normal Probability Distribution Table.
Problem 2
Find out the time required to complete the following project and the critical activities:


Using the
single time estimates of the activities, we get the following network diagram
for the project.


Compare the times for the four paths.
Maximum of {48, 31, 49, 32} = 49.
We see that Path III has the maximum time.
Therefore the critical path is Path III. i.e.,
The critical activities are A, C, E, F and H.
The non-critical activities are B, D, G and I.
Project time (Also called project length) = 49 days.
Problem 3

From the three time estimates tp , tm and to , calculate te for each activity. We obtain the following table:


With the single time estimates of the activities, we get the following network diagram for the project.

Consider the paths, beginning with the start node and stopping with the end node. There are three such paths for the given project. They are as follows:


Calculation of Standard Deviation and Variance for the Critical Activities:

Variance of | project time (Also called
Variance of | project length) = | |||
Sum of the variances for the critical activities
= 1+4+1+ 4/9 = 58/9 Weeks. | |||||
Problem 4
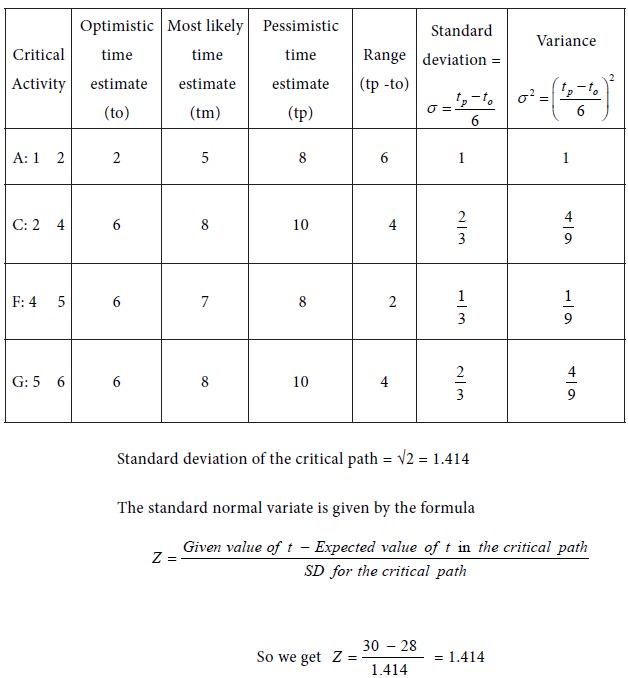
A project consists of seven activities with the following time estimates. Find the probability that the project will be completed in 30 weeks or less.

Solution
From the three time estimates , and , calculate for each activity. The results are furnished in the following table:
From the three time estimates , and , calculate for each activity. The results are furnished in the following table:

With the single time estimates of the activities, the following network diagram is constructed for the project.


Calculation of Standard Deviation and Variance for the Critical Activities:

We refer to the Normal Probability Distribution Table.
Corresponding to Z = 1.414, we
obtain the value of 0.4207
We get 0.5 + 0.4207 = 0. 9207
Therefore the required probability is 0.92
Therefore the required probability is 0.92
i.e.,
There is 92% chance that the project will be completed before 30 weeks. In
other words, the chance that it will be delayed beyond 30 weeks is 8%
Tags : Operations Management - Network Problems
Last 30 days 4355 views












