Operations Management - Game Theory, Goal Programming & Queuing Theory
The concept and Approaches for 2 x n zero-sum game
Posted On :
When the first player A has exactly two strategies and the second player B has n (where n is three or more) strategies, there results a 2 x n game.
The concept of a 2 x n zero-sum game
When the first player A has exactly two strategies and the second player B has n (where n is three or more) strategies, there results a 2 x n game. It is also called a rectangular game. Since A has two strategies only, he cannot try to give up any one of them. However, since B has many strategies, he can make out some choice among them. He can retain some of the advantageous strategies and discard some disadvantageous strategies. The intention of B is to give as minimum payoff to A as possible. In other words, B will always try to minimize the loss to himself. Therefore, if some strategies are available to B by which he can minimize the payoff to A, then B will retain such strategies and give such strategies by which the payoff will be very high to A.
Approaches for 2 x n zero-sum game
There are two approaches for such games: (1) Sub game approach and (2) Graphical approach.
Sub game approach
The given 2 x n game is divided into 2 x 2 sub games. For this purpose, consider all possible 2 x 2 sub matrices of the payoff matrix of the given game. Solve each sub game and have a list of the values of each sub game. Since B can make out a choice of his strategies, he will discard such of those sub games which result in more payoff to A. On the basis of this consideration, in the long run, he will retain two strategies only and give up the other strategies.
Solve the following game

Solution
Let us consider all possible 2x2 sub games of the given game. We have the following sub games:
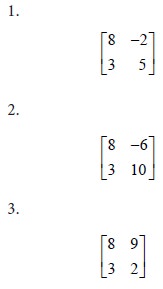
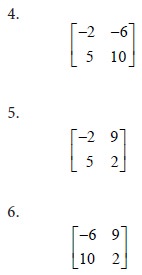
Let E be the expected value of the pay off to player A. Let p be the probability that player A will use his first strategy. Then the probability that he will use his second strategy is 1-p. We form the equations for E in all the sub games as follows:

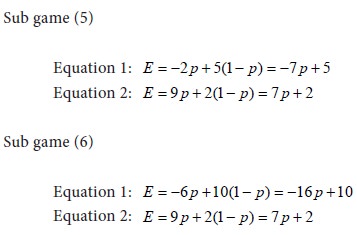
Solve the equations for each sub game. Let us tabulate the results for the various sub games. We have the following:
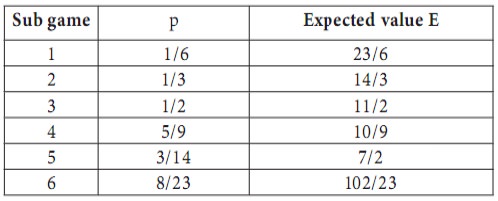
Interpretation
Since player A has only 2 strategies, he cannot make any choice on the strategies. On the other hand, player B has 4 strategies. Therefore he can retain any 2 strategies and give up the other 2 strategies. This he will do in such a way that the pay-off to player A is at the minimum. The pay-off to A is the minimum in the case of sub game 4. i.e., the sub game with the matrix
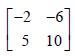
Therefore, in the long run,
player B will retain his strategies 2 and 3 and give up his strategies 1 and 4.
In that case, the probability that A will use his first strategy is p = 5/9 and
the probability that he will use his second strategy is 1-p = 4/9 . i.e., Out
of a total of 9 trials, he will use his first strategy five times and the second
strategy four times. The value of the game is10/9 . The positive sign of V
shows that the game is favourable to player A.
Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 482 views












