Operations Management - Game Theory, Goal Programming & Queuing Theory
Graphical Solution - M X 2 Zero-Sum Games
Posted On :
Now we consider the graphical method of solution to the given game.
Graphical Solution
Now we consider the graphical method of solution to the given game.
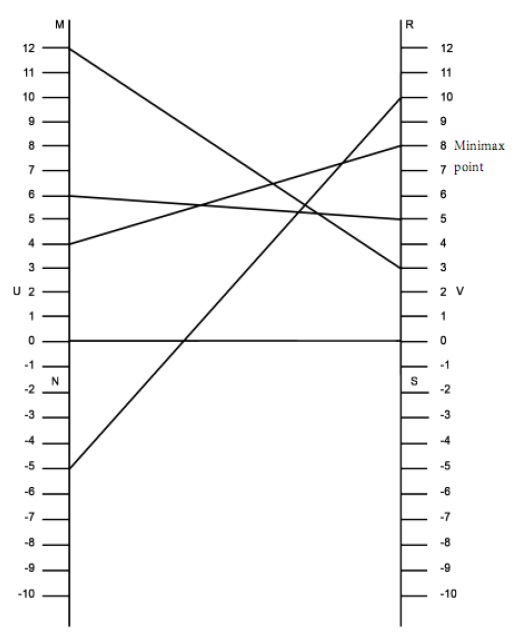
Draw two vertical lines MN and RS. Note that they are parallel to each other. Draw UV perpendicular to MN as well as RS. Take U as the origin on the line MN. Take V as the origin on the line RS.
Mark units on MN and RS with equal scale. The units on the two lines MN and RS are taken as the payoff numbers. The payoffs in the first row of the given matrix are taken along the line MN while the payoffs in the second row are taken along the line RS.
We have to plot the following points: (5, 8), (-2, 10), (12, 4), (6, 5).The points 5, -2, 12, 6 are marked on MN. The points 8, 10, 4, 5 are marked on RS.
Join a point on MN with the corresponding point on RS by a straight line. For example, join the point 5 on MN with the point 8 on RS. We have 4 such straight lines. They represent the 4 moves of the first player. They intersect in 6 points. Take the uppermost point of intersection of the straight lines. It is called the Minimax point. With the help of this point, identify the optimal strategies for the first player. This point corresponds to the points 5 and -2 on MN and 8 and 10 on RS. They correspond to the sub game with the matrix
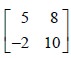
The points 5 and -2 on MN
correspond to the first and second strategies of the first player. Therefore,
the graphical method implies that the first player will retain his strategies 1
and 2 and give up his strategies 3 and 4, in the long run.
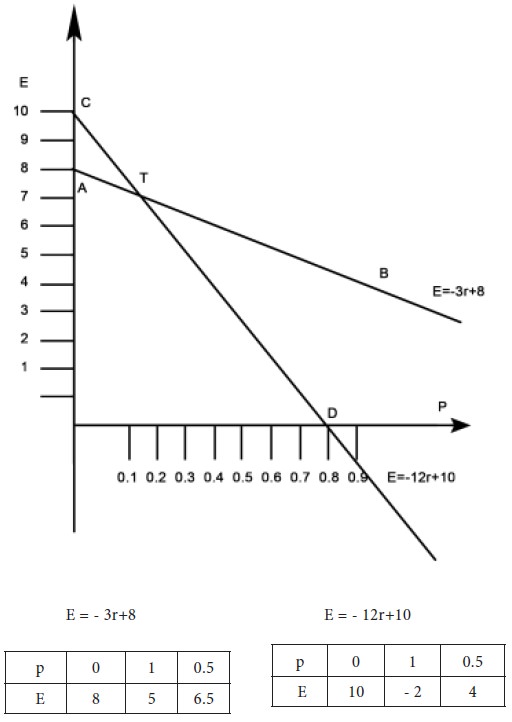
We graphically solve the sub game with the above matrix. We have to solve the two equations E = - 3 r + 8 and E = - 12 r + 10. Represent the two equations by two straight lines AB and CD on the graph sheet. Take the point of intersection of AB and CD as T. For this point, we have r = 2/9 and E = 22/3. Therefore, the value V of the game is 22/3 . We see that the probability that the second player will use his first strategy is r = 2/9 and the probability that he will use his second strategy is 1-r = 7/9 .
Now we consider the graphical method of solution to the given game.
Draw two vertical lines MN and RS. Note that they are parallel to each other. Draw UV perpendicular to MN as well as RS. Take U as the origin on the line MN. Take V as the origin on the line RS.
Mark units on MN and RS with equal scale. The units on the two lines MN and RS are taken as the payoff numbers. The payoffs in the first row of the given matrix are taken along the line MN while the payoffs in the second row are taken along the line RS.
We have to plot the following points: (5, 8), (-2, 10), (12, 4), (6, 5).The points 5, -2, 12, 6 are marked on MN. The points 8, 10, 4, 5 are marked on RS.
Join a point on MN with the corresponding point on RS by a straight line. For example, join the point 5 on MN with the point 8 on RS. We have 4 such straight lines. They represent the 4 moves of the first player. They intersect in 6 points. Take the uppermost point of intersection of the straight lines. It is called the Minimax point. With the help of this point, identify the optimal strategies for the first player. This point corresponds to the points 5 and -2 on MN and 8 and 10 on RS. They correspond to the sub game with the matrix
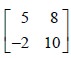
We graphically solve the sub game with the above matrix. We have to solve the two equations E = - 3 r + 8 and E = - 12 r + 10. Represent the two equations by two straight lines AB and CD on the graph sheet. Take the point of intersection of AB and CD as T. For this point, we have r = 2/9 and E = 22/3. Therefore, the value V of the game is 22/3 . We see that the probability that the second player will use his first strategy is r = 2/9 and the probability that he will use his second strategy is 1-r = 7/9 .


Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 946 views












