Home | ARTS | Research Methodology
|
Correction term for ρ when ranks are tied - Correlation And Regression Analysis
Research Methodology - Correlation And Regression Analysis
Correction term for ρ when ranks are tied - Correlation And Regression Analysis
Posted On :
Consider the formula for rank correlation coefficient.
Correction term for ρ when ranks are tied
Consider the formula for rank correlation coefficient. We have
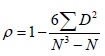
If there is a tie involving m items, we have to add
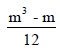
to the term D2 in ρ. We have to add as many terms like (m3 – m) / 12 as there are ties.
Let us calculate the correction terms for certain values of m. These are provided in the following table.
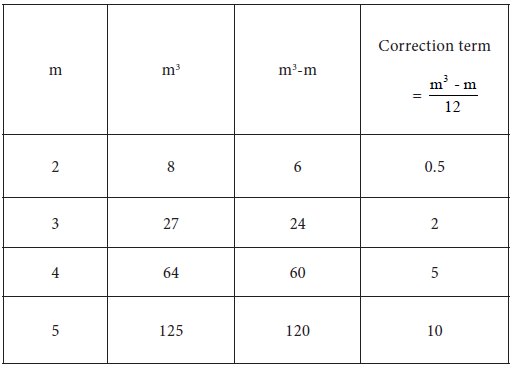
Illustrative examples:
If there is a tie involving 2 items, then the correction term is 0.5
If there are 2 ties involving 2 items each, then the correction term is 0.5 + 0.5 = 1
If there are 3 ties with 2 items each, then the correction term is 0.5 + 0.5 + 0.5 = 1.5
If there is a tie involving 3 items, then the correction term is 2
If there are 2 ties involving 3 items each, then the correction term is 2 + 2 = 4
If there is a tie with 2 items and another tie with 3 items, then the correction term is 0.5 + 2 = 2.5
If there are 2 ties with 2 items each and another tie with 3 items, then the correction term is 0.5 + 0.5 + 2 = 3
Problem 9 : Resolving ties in ranks
The following are the details of ratings scored by two popular insurance schemes. Determine the rank correlation coefficient between them.

Solution:
From the given values, we have to determine the ranks.
Step 1.
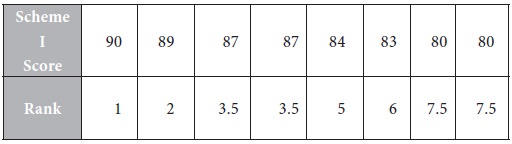
Arrange the scores for Insurance Scheme I in descending order and rank them as 1,2,3,…,8.
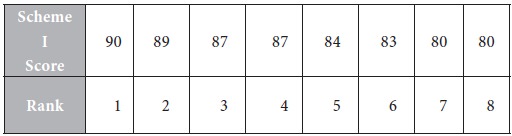
The score 87 appears twice. The corresponding ranks are 3, 4. Their average is (3 + 4) / 2 = 3.5. Assign this rank to the two equal scores in Scheme I.
The score 80 appears twice. The corresponding ranks are 7, 8. Their average is (7 + 8) / 2 = 7.5. Assign this rank to the two equal scores in Scheme I.
The revised ranks for Insurance Scheme I are as follows:
Step 2.
Arrange the scores for Insurance Scheme II in descending order and rank them as 1,2,3,…,8.
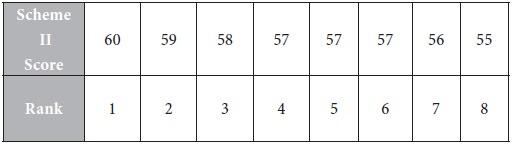
The score 57 appears thrice. The corresponding ranks are 4, 5, 6.
Their average is (4 + 5 + 6) / 3 = 15 / 3 = 5. Assign this rank to the three equal scores in Scheme II.
The revised ranks for Insurance Scheme II are as follows:

Step 3.
Calculation of D2: Assign the revised ranks to the given pairs of values and calculate D2 as follows:
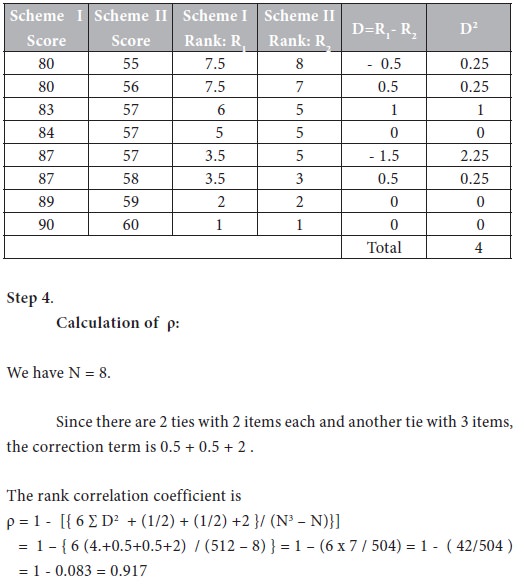
Inference:
Consider the formula for rank correlation coefficient. We have
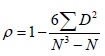
If there is a tie involving m items, we have to add
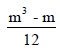
to the term D2 in ρ. We have to add as many terms like (m3 – m) / 12 as there are ties.
Let us calculate the correction terms for certain values of m. These are provided in the following table.

Illustrative examples:
If there is a tie involving 2 items, then the correction term is 0.5
If there are 2 ties involving 2 items each, then the correction term is 0.5 + 0.5 = 1
If there are 3 ties with 2 items each, then the correction term is 0.5 + 0.5 + 0.5 = 1.5
If there is a tie involving 3 items, then the correction term is 2
If there are 2 ties involving 3 items each, then the correction term is 2 + 2 = 4
If there is a tie with 2 items and another tie with 3 items, then the correction term is 0.5 + 2 = 2.5
If there are 2 ties with 2 items each and another tie with 3 items, then the correction term is 0.5 + 0.5 + 2 = 3
Problem 9 : Resolving ties in ranks
The following are the details of ratings scored by two popular insurance schemes. Determine the rank correlation coefficient between them.

Solution:
From the given values, we have to determine the ranks.
Step 1.
Arrange the scores for Insurance Scheme I in descending order and rank them as 1,2,3,…,8.

The score 87 appears twice. The corresponding ranks are 3, 4. Their average is (3 + 4) / 2 = 3.5. Assign this rank to the two equal scores in Scheme I.
The score 80 appears twice. The corresponding ranks are 7, 8. Their average is (7 + 8) / 2 = 7.5. Assign this rank to the two equal scores in Scheme I.
The revised ranks for Insurance Scheme I are as follows:

Step 2.
Arrange the scores for Insurance Scheme II in descending order and rank them as 1,2,3,…,8.

The score 57 appears thrice. The corresponding ranks are 4, 5, 6.
Their average is (4 + 5 + 6) / 3 = 15 / 3 = 5. Assign this rank to the three equal scores in Scheme II.
The revised ranks for Insurance Scheme II are as follows:

Step 3.
Calculation of D2: Assign the revised ranks to the given pairs of values and calculate D2 as follows:

Inference:
It
is inferred that the two insurance schemes are highly, positively correlated.
Tags : Research Methodology - Correlation And Regression Analysis
Last 30 days 566 views












