Research Methodology - Introduction
Concepts Relating To Testing Of Hypotheses
Posted On :
Testing of hypotheses requires a researcher to be familiar with various concepts concerned with it such as:
Concepts Relating To Testing Of Hypotheses:
Testing of hypotheses requires a researcher to be familiar with various concepts concerned with it such as:
In the context of statistical analysis, hypotheses are of two types viz., null hypothesis and alternative hypothesis. When two methods A and B are compared on their relative superiority, and it is assumed that both the methods are equally good, then such a statement is called as the null hypothesis. On the other hand, if method A is considered relatively superior to method B, or vice-versa, then such a statement is known as an alternative hypothesis. The null hypothesis is expressed as H0, while the alternative hypothesis is expressed as Ha. For example, if a researcher wants to test the hypothesis that the population mean (μ) is equal to the hypothesized mean (H0) = 100, then the null hypothesis should be stated as the population mean is equal to the hypothesized mean 100. Symbolically it may be written as:-
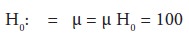
If sample results do not support this null hypothesis, then it should be concluded that something else is true. The conclusion of rejecting the null hypothesis is called as alternative hypothesis H1. To put it in simple words, the set of alternatives to the null hypothesis is termed as the alternative hypothesis. If H0 is accepted, then it implies that Ha is being rejected. On the other hand, if H0 is rejected, it means that Ha is being accepted. For H0: μ = μ H0 = 100, the following three possible alternative hypotheses may be considered:
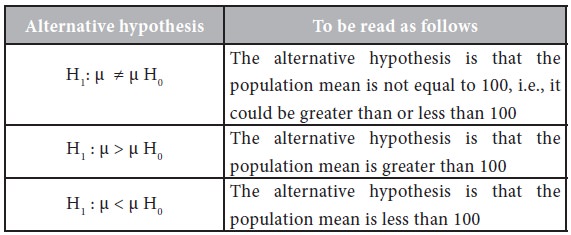
Before the sample is drawn, the researcher has to state the null hypothesis and the alternative hypothesis. While formulating the null hypothesis, the following aspects need to be considered:
1. Alternative hypothesis is usually the one which a researcher wishes to prove, whereas the null hypothesis is the one which he/she wishes to disprove. Thus, a null hypothesis is usually the one which a researcher tries to reject, while an alternative hypothesis is the one that represents all other possibilities.
2. The rejection of a hypothesis when it is actually true involves great risk, as it indicates that it is a null hypothesis because then the probability of rejecting it when it is true is α (i.e., the level of significance) which is chosen very small.
3. Null hypothesis should always be specific hypothesis i.e., it should not state about or approximately a certain value.
In the context of hypothesis testing, the level of significance is a very important concept. It is a certain percentage that should be chosen with great care, reason and insight. If for instance, the significance level is taken at 5 per cent, then it means that H0 would be rejected when the sampling result has a less than 0.05 probability of occurrence when H0 is true. In other words, the five per cent level of significance implies that the researcher is willing to take a risk of five per cent of rejecting the null hypothesis, when (H0) is actually true. In sum, the significance level reflects the maximum value of the probability of rejecting H0 when it is actually true, and which is usually determined prior to testing the hypothesis.
Suppose the given hypothesis is H0 and the alternative hypothesis H1, then the researcher has to make a rule known as the decision rule. According to the decision rule, the researcher accepts or rejects H0. For example, if the H0 is that certain students are good against the H1 that all the students are good, then the researcher should decide the number of items to be tested and the criteria on the basis of which to accept or reject the hypothesis.
As regards the testing of hypotheses, a researcher can make basically two types of errors. He/she may reject H0 when it is true, or accept H0 when it is not true. The former is called as Type I error and the latter is known as Type II error. In other words, Type I error implies the rejection of a hypothesis when it must have been accepted, while Type II error implies the acceptance of a hypothesis which must have been rejected. Type I error is denoted by α (alpha) and is known as α error, while Type II error is usually denoted by β (beta) and is known as β error.
These two types of tests are very
important in the context of hypothesis testing. A two-tailed test rejects the
null hypothesis, when the sample mean is significantly greater or lower than
the hypothesized value of the mean of the population. Such a test is suitable
when the null hypothesis is some specified value, the alternative hypothesis is
a value that is not equal to the specified value of the null hypothesis.
Testing of hypotheses requires a researcher to be familiar with various concepts concerned with it such as:
Null Hypothesis And Alternative Hypothesis:
In the context of statistical analysis, hypotheses are of two types viz., null hypothesis and alternative hypothesis. When two methods A and B are compared on their relative superiority, and it is assumed that both the methods are equally good, then such a statement is called as the null hypothesis. On the other hand, if method A is considered relatively superior to method B, or vice-versa, then such a statement is known as an alternative hypothesis. The null hypothesis is expressed as H0, while the alternative hypothesis is expressed as Ha. For example, if a researcher wants to test the hypothesis that the population mean (μ) is equal to the hypothesized mean (H0) = 100, then the null hypothesis should be stated as the population mean is equal to the hypothesized mean 100. Symbolically it may be written as:-
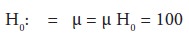
If sample results do not support this null hypothesis, then it should be concluded that something else is true. The conclusion of rejecting the null hypothesis is called as alternative hypothesis H1. To put it in simple words, the set of alternatives to the null hypothesis is termed as the alternative hypothesis. If H0 is accepted, then it implies that Ha is being rejected. On the other hand, if H0 is rejected, it means that Ha is being accepted. For H0: μ = μ H0 = 100, the following three possible alternative hypotheses may be considered:

Before the sample is drawn, the researcher has to state the null hypothesis and the alternative hypothesis. While formulating the null hypothesis, the following aspects need to be considered:
1. Alternative hypothesis is usually the one which a researcher wishes to prove, whereas the null hypothesis is the one which he/she wishes to disprove. Thus, a null hypothesis is usually the one which a researcher tries to reject, while an alternative hypothesis is the one that represents all other possibilities.
2. The rejection of a hypothesis when it is actually true involves great risk, as it indicates that it is a null hypothesis because then the probability of rejecting it when it is true is α (i.e., the level of significance) which is chosen very small.
3. Null hypothesis should always be specific hypothesis i.e., it should not state about or approximately a certain value.
The Level Of Significance:
In the context of hypothesis testing, the level of significance is a very important concept. It is a certain percentage that should be chosen with great care, reason and insight. If for instance, the significance level is taken at 5 per cent, then it means that H0 would be rejected when the sampling result has a less than 0.05 probability of occurrence when H0 is true. In other words, the five per cent level of significance implies that the researcher is willing to take a risk of five per cent of rejecting the null hypothesis, when (H0) is actually true. In sum, the significance level reflects the maximum value of the probability of rejecting H0 when it is actually true, and which is usually determined prior to testing the hypothesis.
Test Of Hypothesis Or Decision Rule:
Suppose the given hypothesis is H0 and the alternative hypothesis H1, then the researcher has to make a rule known as the decision rule. According to the decision rule, the researcher accepts or rejects H0. For example, if the H0 is that certain students are good against the H1 that all the students are good, then the researcher should decide the number of items to be tested and the criteria on the basis of which to accept or reject the hypothesis.
Type I And Type II Errors:
As regards the testing of hypotheses, a researcher can make basically two types of errors. He/she may reject H0 when it is true, or accept H0 when it is not true. The former is called as Type I error and the latter is known as Type II error. In other words, Type I error implies the rejection of a hypothesis when it must have been accepted, while Type II error implies the acceptance of a hypothesis which must have been rejected. Type I error is denoted by α (alpha) and is known as α error, while Type II error is usually denoted by β (beta) and is known as β error.
One-Tailed And Two-Tailed Tests:
Tags : Research Methodology - Introduction
Last 30 days 1177 views












