Home | ARTS | Operations Management
|
Problem of Graphical Solution Of A 2X2 Game With No Saddle Point
Operations Management - Game Theory, Goal Programming & Queuing Theory
Problem of Graphical Solution Of A 2X2 Game With No Saddle Point
Posted On :
Solve the following game by graphical method.
Problem
Solve the following game by graphical method.

Solution
First consider the row minima
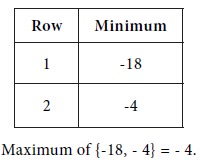
Next, consider the column maxima
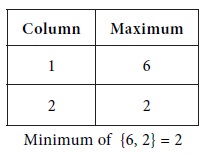
We see that Maximum { row minima} ≠ Minimum { column maxima }
So, the game has no saddle point. It is a mixed game.
Let p be the probability that player A will use his first strategy.
Then the probability that A will use his second strategy is 1-p.
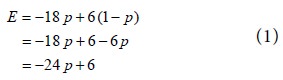
When B uses his second strategy The expected value of pay-off to player A is given by
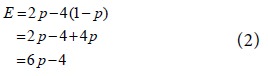
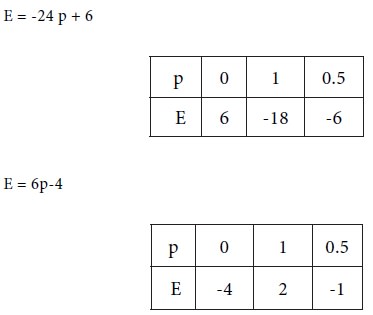
Consider equations (1) and (2). For plotting the two equations on a
graph sheet, get some points on them as follows:
Graphical
solution
Take probability and expected value along two rectangular axes in a graph sheet. Draw two straight lines given by the two equations (1) and (2). Determine the point of intersection of the two straight lines in the graph. This will provide the common solution of the two equations (1) and (2). Thus we would get the value of the game.
Solve the following game by graphical method.

Solution
First consider the row minima

Next, consider the column maxima

We see that Maximum { row minima} ≠ Minimum { column maxima }
So, the game has no saddle point. It is a mixed game.
Let p be the probability that player A will use his first strategy.
Then the probability that A will use his second strategy is 1-p.
When B uses his first strategy
The expected value of pay-off to player A is given by
The expected value of pay-off to player A is given by
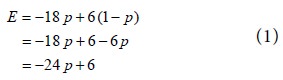
When B uses his second strategy The expected value of pay-off to player A is given by
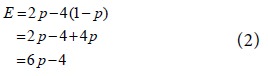

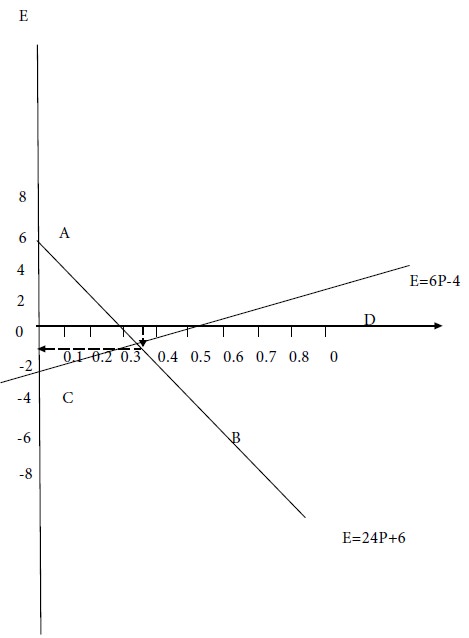
Take probability and expected value along two rectangular axes in a graph sheet. Draw two straight lines given by the two equations (1) and (2). Determine the point of intersection of the two straight lines in the graph. This will provide the common solution of the two equations (1) and (2). Thus we would get the value of the game.
Represent the two equations by the two straight lines AB and CD on the graph sheet. Take the point of intersection of AB and CD as T. For this point, we have p = 1/3 and E = -2. Therefore, the value V of the game is -2.
Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 1409 views












