Home | ARTS | Operations Management
|
Solve a game by simplex method - Linear Programming Approach To Game Theory
Operations Management - Game Theory, Goal Programming & Queuing Theory
Solve a game by simplex method - Linear Programming Approach To Game Theory
Posted On :
Solve the following game by simplex method for LPP:
Solve a game by simplex method
Solve the following game by simplex method for LPP:
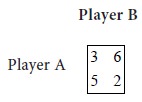
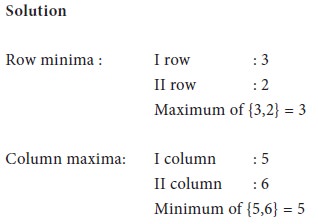
So, Maximum of {Row minima} ≠ Minimum of {Column maxima}.
Therefore the given game has no saddle point. It is a mixed game.
Let us convert the given game into a LPP.
Let V denote the value of the game. Let the probability that the player B will use his first strategy be r and second strategy be s. Let V denote the value of the game.
When A follows his first strategy
The expected payoff to A (i.e., the expected loss to B) = 3 r + 6 s.
This pay-off cannot exceed V. So we have =3 r + 6 s V (1)
When A follows his second strategy
The expected pay-off to A (i.e., expected loss to B) = 5 r + 2 s.
This cannot exceed V. Hence we obtain the condition = 5 r + 2 s V (2)
From (1) and (2) we have


Consider the negative elements in the objective function row. They are –1, -1. The absolute values are 1, 1. There is a tie between these coefficients. To resolve the tie, we select the variable x. We take the new basic variable as x. Consider the ratio of b-value to x-value. We have the following ratios:


Solve the following game

Solution
The game has no saddle point. It is a mixed game. Let the probability that B will use his first strategy be r. Let the probability that B will use his second strategy be s. Let V be the value of the game.
When A follows his first strategy
The expected payoff to A (i.e., the expected loss to B) = 2 r +5 s.
The pay-off to A cannot exceed V. So we have = 2 r + 5 s V (I)
When A follows his second strategy
The expected pay-off to A (i.e., expected loss to B) = 4 r + s.
The pay-off to A cannot exceed V. Hence we obtain the condition = 4 r + s V (II)
From (I) and (II) we have

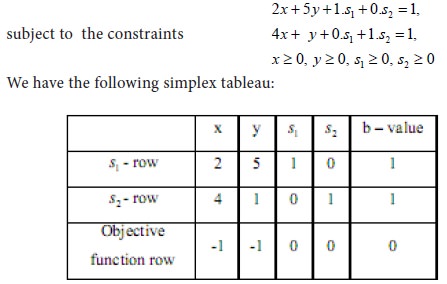
Consider the negative elements in the objective function row. They are –1, -1. The absolute value are 1, 1. There is a tie between these coefficients. To resolve the tie, we select the variable x. We take the new basic variable as x. Consider the ratio of b-value to x-value. We have the following ratios:


Solve the following game by simplex method for LPP
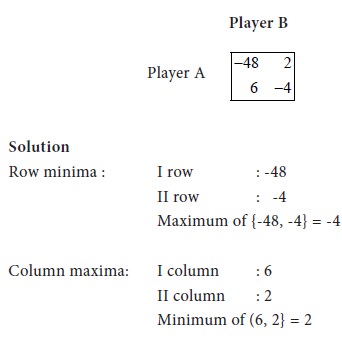
So, Maximum of {Row minima} ≠ Minimum of {Column maxima}.
Therefore the given game has no saddle point. It is a mixed game. Let us convert the given game into a LPP.
Let V denote the value of the game. Let the probability that the player B will use his first strategy be r and second strategy be s. Let V denote the value of the game.
When A follows his second strategy
The expected pay-off to A (i.e., expected loss to B) = 6 r - 4 s.


Consider the negative elements in the objective function row. They are –1, -1. The absolute value are 1, 1. There is a tie between these coefficients. To resolve the tie, we select the variable x. We take the new basic variable as x. Consider the ratio of b-value to x-value. We have the following ratios:


Transform the following game into an LPP
s = 9/10
Solution
We have to determine the optimal strategy for player B. Using the entries of the given matrix, we obtain the inequalities

Problem 1
Solve the following game by simplex method for LPP:


So, Maximum of {Row minima} ≠ Minimum of {Column maxima}.
Therefore the given game has no saddle point. It is a mixed game.
Let us convert the given game into a LPP.
Problem formulation
Let V denote the value of the game. Let the probability that the player B will use his first strategy be r and second strategy be s. Let V denote the value of the game.
When A follows his first strategy
The expected payoff to A (i.e., the expected loss to B) = 3 r + 6 s.
This pay-off cannot exceed V. So we have =3 r + 6 s V (1)
When A follows his second strategy
The expected pay-off to A (i.e., expected loss to B) = 5 r + 2 s.
This cannot exceed V. Hence we obtain the condition = 5 r + 2 s V (2)
From (1) and (2) we have

Solution of LPP

Consider the negative elements in the objective function row. They are –1, -1. The absolute values are 1, 1. There is a tie between these coefficients. To resolve the tie, we select the variable x. We take the new basic variable as x. Consider the ratio of b-value to x-value. We have the following ratios:


Problem 2
Solve the following game

The game has no saddle point. It is a mixed game. Let the probability that B will use his first strategy be r. Let the probability that B will use his second strategy be s. Let V be the value of the game.
The expected payoff to A (i.e., the expected loss to B) = 2 r +5 s.
The pay-off to A cannot exceed V. So we have = 2 r + 5 s V (I)
The expected pay-off to A (i.e., expected loss to B) = 4 r + s.
The pay-off to A cannot exceed V. Hence we obtain the condition = 4 r + s V (II)
From (I) and (II) we have


Consider the negative elements in the objective function row. They are –1, -1. The absolute value are 1, 1. There is a tie between these coefficients. To resolve the tie, we select the variable x. We take the new basic variable as x. Consider the ratio of b-value to x-value. We have the following ratios:


Problem 3
Solve the following game by simplex method for LPP

So, Maximum of {Row minima} ≠ Minimum of {Column maxima}.
Therefore the given game has no saddle point. It is a mixed game. Let us convert the given game into a LPP.
Problem formulation
Let V denote the value of the game. Let the probability that the player B will use his first strategy be r and second strategy be s. Let V denote the value of the game.
When A follows his first strategy | ||
The expected payoff to A (i.e., the expected loss to B) = | - 48 r + 2 s. | |
This pay-off cannot exceed V. So we have =- 48 r + 2 s | V | (1)’ |
When A follows his second strategy
The expected pay-off to A (i.e., expected loss to B) = 6 r - 4 s.
This cannot exceed V. Hence we obtain the condition = 6 r - 4 s V (2)’


Consider the negative elements in the objective function row. They are –1, -1. The absolute value are 1, 1. There is a tie between these coefficients. To resolve the tie, we select the variable x. We take the new basic variable as x. Consider the ratio of b-value to x-value. We have the following ratios:


Problem 4
Transform the following game into an LPP
s = 9/10
Solution
We have to determine the optimal strategy for player B. Using the entries of the given matrix, we obtain the inequalities

Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 1811 views












