Operations Management - Game Theory, Goal Programming & Queuing Theory
Problem of Two-Person Zero Sum Games
Posted On :
Solve the game with the following pay-off matrix.
Problem 1
Solve the game with the following pay-off matrix.
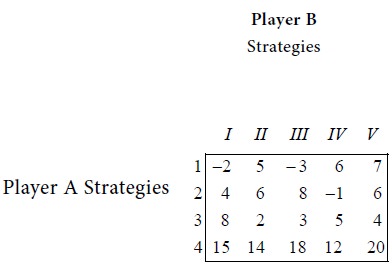
Solution
First consider the minimum of each row.
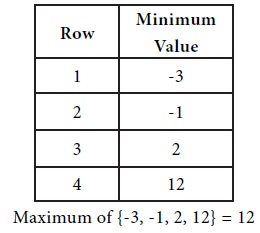
Next consider the maximum of each column.
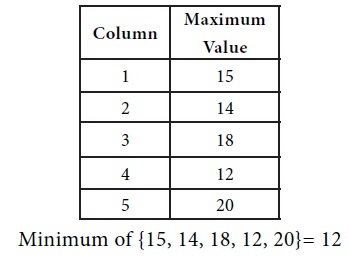
We see that the maximum of row minima = the minimum of the column maxima. So the game has a saddle point. The common value is 12. Therefore the value V of the game = 12.
Interpretation
In the long run, the following best strategies will be identified by the two players:
The best strategy for player A is strategy 4.
The best strategy for player B is strategy IV.
The game is favourable to player A.
Problem 2
Solve the game with the following pay-off matrix
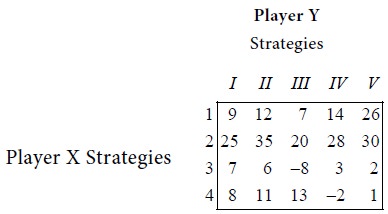
Solution
First consider the minimum of each row.
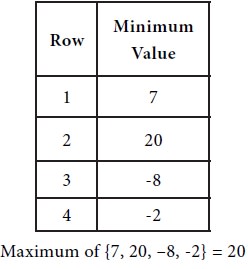
Next consider the maximum of each column.
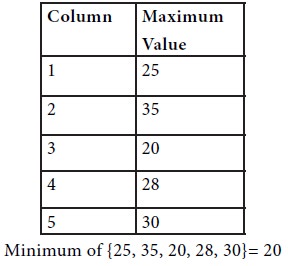
It is observed that the maximum of row minima and the minimum of the column maxima are equal. Hence the given the game has a saddle point. The common value is 20. This indicates that the value V of the game is 20.
Interpretation.
The best strategy for player X is strategy 2.
The best strategy for player Y is strategy III.
The game is favourable to player A.
Problem 3

Solution
First consider the minimum of each row.
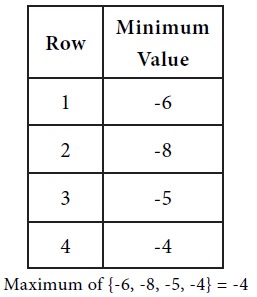
Next consider the maximum of each column.
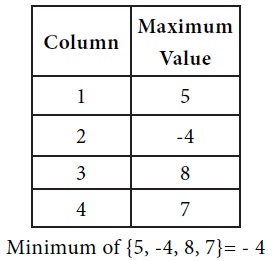
Since the max {row minima} = min {column maxima}, the game under consideration has a saddle point. The common value is –4. Hence the value of the game is –4.
Interpretation
The best strategy for player A is strategy 4.
The best strategy for player B is strategy II.
Since the value of the game is negative, it is concluded that the game is favourable to player B.
Solve the game with the following pay-off matrix.

Solution
First consider the minimum of each row.

Next consider the maximum of each column.

We see that the maximum of row minima = the minimum of the column maxima. So the game has a saddle point. The common value is 12. Therefore the value V of the game = 12.
Interpretation
In the long run, the following best strategies will be identified by the two players:
The best strategy for player A is strategy 4.
The best strategy for player B is strategy IV.
The game is favourable to player A.
Problem 2
Solve the game with the following pay-off matrix

Solution
First consider the minimum of each row.

Next consider the maximum of each column.

It is observed that the maximum of row minima and the minimum of the column maxima are equal. Hence the given the game has a saddle point. The common value is 20. This indicates that the value V of the game is 20.
Interpretation.
The best strategy for player X is strategy 2.
The best strategy for player Y is strategy III.
The game is favourable to player A.
Problem 3
Solve the following game:

Solution
First consider the minimum of each row.

Next consider the maximum of each column.

Since the max {row minima} = min {column maxima}, the game under consideration has a saddle point. The common value is –4. Hence the value of the game is –4.
Interpretation
The best strategy for player A is strategy 4.
The best strategy for player B is strategy II.
Since the value of the game is negative, it is concluded that the game is favourable to player B.
Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 1113 views












