Operations Management - Network Problems
Problem of Crashing Of A Project
Posted On :
A project has activities with the following normal and crash times and cost:
Problem 1
A project has activities with the following normal and crash times and cost:
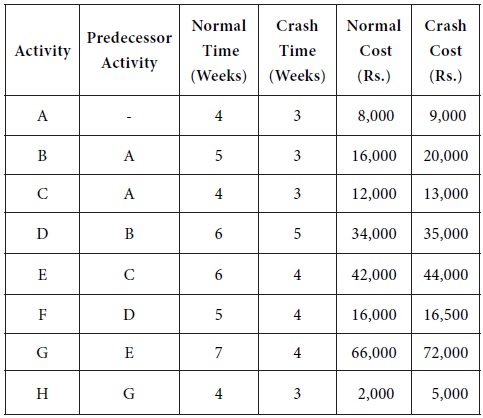
Determine
a crashing scheme for the above project so that the total project time is
reduced by 3 weeks.
Solution
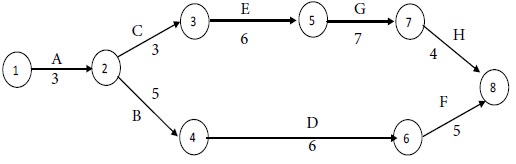
We have the following network diagram for the given project with normal costs:
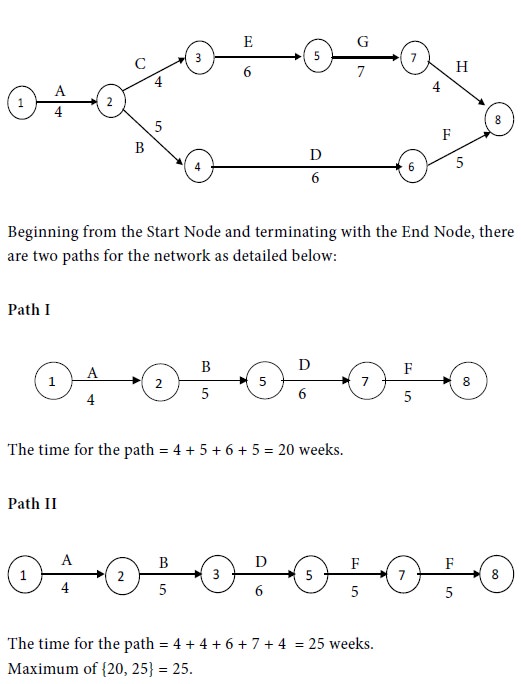
Therefore
Path II is the critical path and the critical activities are A, C, E, G and H.
The non-critical activities are B, D and F.
A non-critical
activity can be delayed without delaying the execution of the whole project.
But, if a critical activity is delayed, it will delay the whole project.
Because of this reason, we have to select a critical activity for crashing.
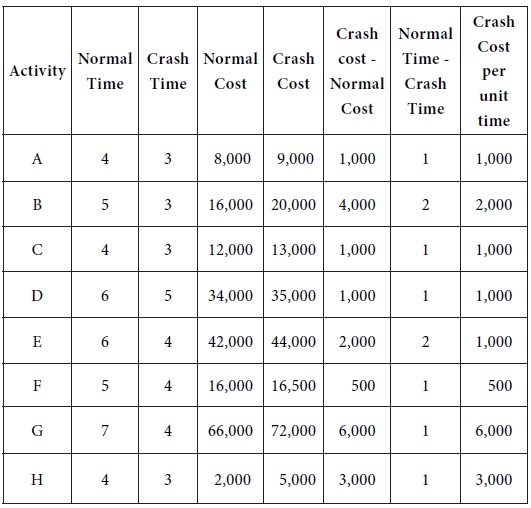
Here we have to choose one of the activities A, C, E, G and H The crash cost
per unit time works out as follows:
Rs. 1,000
for A; Rs. 1,000 for C; Rs. 1,000 for E; Rs. 6,000 for G; Rs. 3,000 for H.
The maximum among them is Rs. 1,000. So we have to choose an activity with Rs.1,000 as the crash cost per unit time. However, there is a tie among A, C and E. The tie can be resolved arbitrarily. Let us select A for crashing. We reduce the time of A by one week by spending an extra amount of Rs. 1,000.
After this step, we have the following network with the revised times for the activities:
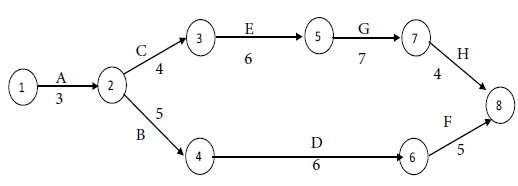
The revised time for Path I = 3 + 5 + 6 + 5 = 19
weeks.
The time for Path II = 3 + 4 + 6 + 7 + 4 = 24 weeks.
Maximum of {19, 24} = 24.
Therefore Path II is the critical path and the critical activities are A, C, E, G and H. However, the time for A cannot be reduced further. Therefore, we have to consider C, E, G and H for crashing. Among them, C and E have the least crash cost per unit time. The tie between C and E can be resolved arbitrarily. Suppose we reduce the time of C by one week with an extra cost of Rs. 1,000.
After
this step, we have the following network with the revised times for the
activities:
The time for Path I = 3 + 5 + 6 +
5 = 19 weeks.
The time for Path II = 3 + 3 + 6 + 7 + 4 = 23 weeks.
Maximum of {19, 23} = 23.
Therefore Path II is the critical path and the critical activities are A, C, E, G and H. Now the time for A or C cannot be reduced further. Therefore, we have to consider E, G and H for crashing. Among them, E has the least crash cost per unit time. Hence we reduce the time of E by one week with an extra cost of Rs. 1,000.
By the given condition, we have to reduce the project time by 3 weeks. Since this has been accomplished, we stop with this step.
Result: We have arrived at the following crashing scheme for the given project:
Reduce the time of A, C and E by one week each.
Project time after crashing is 22 weeks.
Extra amount required = 1,000 + 1,000 + 1,000 = Rs. 3,000.
Problem 2
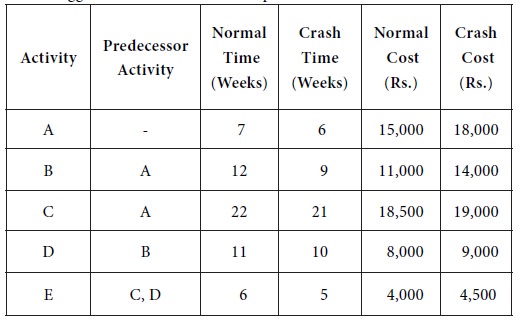
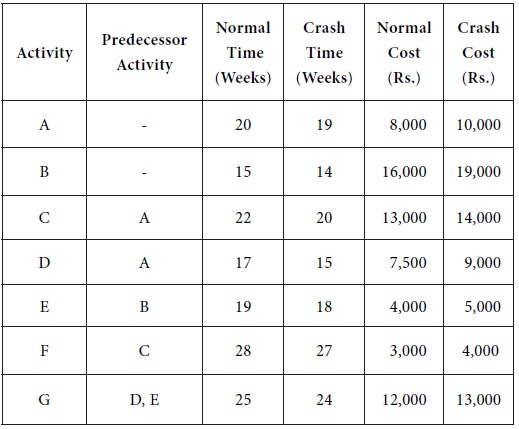
The management of a company is interested in crashing of the following project by spending an additional amount not exceeding Rs. 2,000. Suggest how this can be accomplished.
Solution
We have the following network diagram for the given project with normal costs:
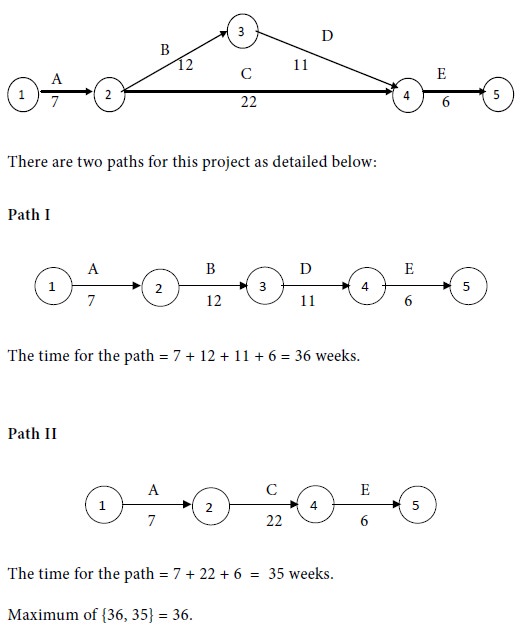
Therefore
Path I is the critical path and the critical activities are A, B, D and E. The
non-critical activity is C.
The crash cost per unit time for the activities in the project are provided in the following table.
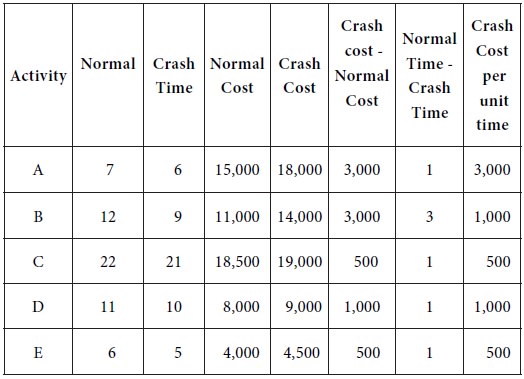
We have to choose one of the activities A, B, D and E for crashing. The crash cost per unit time is as follows:
Rs. 3,000 for A; Rs. 1,000 for B; Rs. 1,000 for D; Rs. 500 for E.
The least among them is Rs. 500. So we have to choose the activity E for crashing. We reduce the time of E by one week by spending an extra amount of Rs. 500.
After this step, we have the following network with the revised times for the activities:
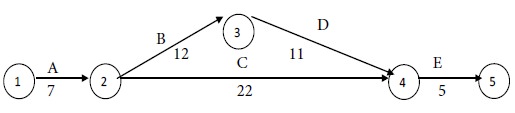
The revised time for Path I = 7 +
12 + 11 + 5 = 35 weeks.
The time for Path II = 7 + 22 + 5 = 34 weeks.
Maximum of {35, 34} = 35.
Therefore Path I is the critical path and the critical activities are A, B, D and E. The non-critical activity is C.
The time of E cannot be reduced further. So we cannot select it for crashing. Next B and have the smallest crash cost per unit time. Let us select B for crashing. Let us reduce the time of E by one week at an extra cost of Rs. 1,000.
After this step, we have the following network with the revised times for the activities:
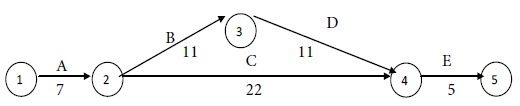
The revised time for Path I = 7 + 11 + 11 + 5 = 34
weeks.
The time for Path II = 7 + 22 + 5 = 34 weeks.
Maximum of {34, 34} = 34.
Since both paths have equal times, both are critical paths. So, we can choose an activity for crashing from either of them depending on the least crash cost per unit time. In path I, the activities are A, B, D and E. In path II, the activities are A, C and E.
The crash cost per unit time is the least for activity C. So we select C for crashing. Reduce the time of C by one week at an extra cost of Rs. 500.
By the given condition, the extra amount cannot exceed Rs. 2,000.
Since this state has been met, we stop with this step.
Result: The following crashing scheme is suggested for the given project:
Reduce the time of E, B and C by one week each.
Project time after crashing is 33 weeks.
Extra amount required = 500 + 1,000 + 500 = Rs. 2,000.
Problem 3
The manager of a company wants to apply crashing for the following project by spending an additional amount not exceeding Rs. 2,000. Offer your suggestion to the manager.
Solution
We have the following network diagram for the given project with normal costs:
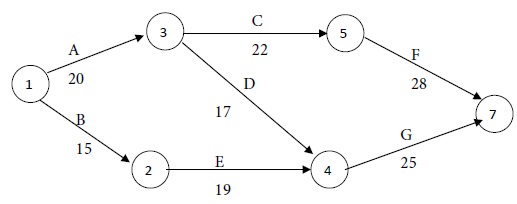
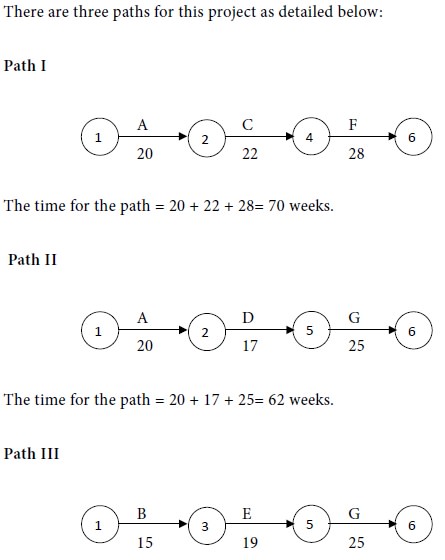
The time for the path = 15+19 +25 = 69 weeks.
Maximum of {70, 62, 69} = 70.
Therefore Path I is the critical path and the critical activities are A, C and F. The non-critical activities are B, D, E and G.
The crash cost per unit time for the activities in the project are provided in the following table
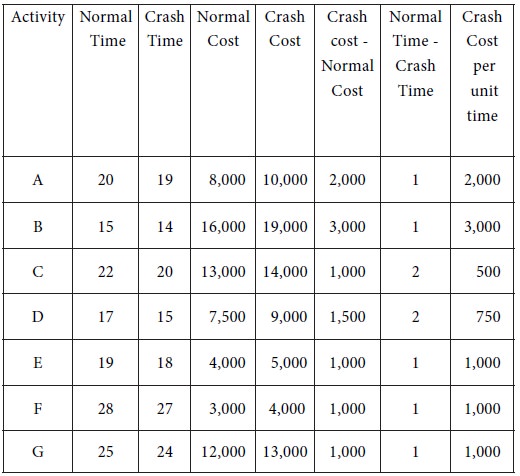
We have to choose one of the activities A, C and F for crashing. The crash cost per unit time is as follows:
Rs. 2,000 for A; Rs. 500 for C; Rs. 1,000 for F.
The least among them is Rs. 500. So we have to choose the activity C for crashing. We reduce the time of C by one week by spending an extra amount of Rs. 500.
After this step, we have the following network with the revised times for the activities:
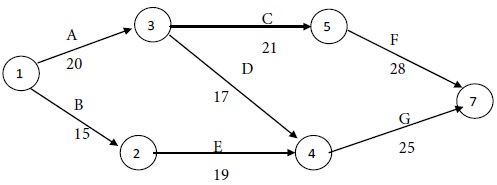
The revised time for Path I = 20 + 21 + 28= 69
weeks.
The time for Path II = 20 + 17 + 25= 62 weeks.
The time for Path III = 15+19 +25 = 69 weeks.
Maximum of {69, 62, 69} = 69.
Since paths I and III have equal times, both are critical paths. So, we can choose an activity for crashing from either of them depending on the least crash cost per unit time.
In path I, the activities are A, C and F. In path III, the activities are B, E and G.
The crash cost per unit time is the least for activity C. So we select C for crashing. Reduce the time of C by one week at an extra cost of Rs. 500.
After this step, we have the following network with the revised times for the activities:
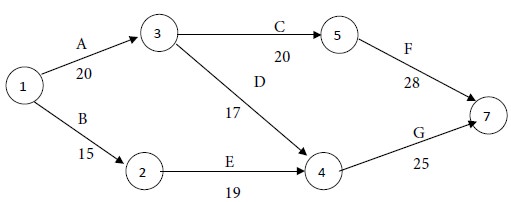
The revised time for Path I = 20 + 20 + 28= 68
weeks.
The time for Path II = 20 + 17 + 25= 62 weeks.
The time for Path III = 15+19 +25 = 69 weeks.
Maximum of {68, 62, 69} = 69.
Therefore path III is the critical activities. Hence we have to select an activity from Path III for crashing. We see that the crash cost per unit time is as follows:
Rs. 3,000 for B; Rs. 1,000 for E; Rs. 1,000 for G.
The least among them is Rs. 1,000. So we can select either E or G for crashing. Let us select E for crashing. We reduce the time of E by one week by spending an extra amount of Rs. 1,000.
By the given condition, the extra amount cannot exceed Rs. 2,000.
Since this condition has been reached, we stop with this step.
Result: The following crashing scheme is suggested for the given project: Reduce the time of C by 2 weeks and that of E by one week.
Project time after crashing is 67 weeks.
Extra amount required = 2 x 500 + 1,000 = Rs. 2,000.
A project has activities with the following normal and crash times and cost:

Solution
We have the following network diagram for the given project with normal costs:

Given that the normal time of activity A is 4 weeks
while its crash time is 3 weeks. Hence the time of this activity can be reduced
by one week if the management is prepared to spend an additional amount.
However, the time cannot be reduced by more than one week even if the
management may be prepared to spend more money. The normal cost of this
activity is Rs. 8,000 whereas the crash cost is Rs. 9,000. From this, we see
that crashing of activity A by one week will cost the management an extra
amount of Rs. 1,000. In a similar fashion, we can work out the crash cost per
unit time for the other activities also. The results are provided in the
following table.

The maximum among them is Rs. 1,000. So we have to choose an activity with Rs.1,000 as the crash cost per unit time. However, there is a tie among A, C and E. The tie can be resolved arbitrarily. Let us select A for crashing. We reduce the time of A by one week by spending an extra amount of Rs. 1,000.
After this step, we have the following network with the revised times for the activities:

The time for Path II = 3 + 4 + 6 + 7 + 4 = 24 weeks.
Maximum of {19, 24} = 24.
Therefore Path II is the critical path and the critical activities are A, C, E, G and H. However, the time for A cannot be reduced further. Therefore, we have to consider C, E, G and H for crashing. Among them, C and E have the least crash cost per unit time. The tie between C and E can be resolved arbitrarily. Suppose we reduce the time of C by one week with an extra cost of Rs. 1,000.

The time for Path II = 3 + 3 + 6 + 7 + 4 = 23 weeks.
Maximum of {19, 23} = 23.
Therefore Path II is the critical path and the critical activities are A, C, E, G and H. Now the time for A or C cannot be reduced further. Therefore, we have to consider E, G and H for crashing. Among them, E has the least crash cost per unit time. Hence we reduce the time of E by one week with an extra cost of Rs. 1,000.
By the given condition, we have to reduce the project time by 3 weeks. Since this has been accomplished, we stop with this step.
Result: We have arrived at the following crashing scheme for the given project:
Reduce the time of A, C and E by one week each.
Project time after crashing is 22 weeks.
Extra amount required = 1,000 + 1,000 + 1,000 = Rs. 3,000.
Problem 2
The management of a company is interested in crashing of the following project by spending an additional amount not exceeding Rs. 2,000. Suggest how this can be accomplished.

We have the following network diagram for the given project with normal costs:

The crash cost per unit time for the activities in the project are provided in the following table.

We have to choose one of the activities A, B, D and E for crashing. The crash cost per unit time is as follows:
Rs. 3,000 for A; Rs. 1,000 for B; Rs. 1,000 for D; Rs. 500 for E.
The least among them is Rs. 500. So we have to choose the activity E for crashing. We reduce the time of E by one week by spending an extra amount of Rs. 500.
After this step, we have the following network with the revised times for the activities:

The time for Path II = 7 + 22 + 5 = 34 weeks.
Maximum of {35, 34} = 35.
Therefore Path I is the critical path and the critical activities are A, B, D and E. The non-critical activity is C.
The time of E cannot be reduced further. So we cannot select it for crashing. Next B and have the smallest crash cost per unit time. Let us select B for crashing. Let us reduce the time of E by one week at an extra cost of Rs. 1,000.
After this step, we have the following network with the revised times for the activities:

The time for Path II = 7 + 22 + 5 = 34 weeks.
Maximum of {34, 34} = 34.
Since both paths have equal times, both are critical paths. So, we can choose an activity for crashing from either of them depending on the least crash cost per unit time. In path I, the activities are A, B, D and E. In path II, the activities are A, C and E.
The crash cost per unit time is the least for activity C. So we select C for crashing. Reduce the time of C by one week at an extra cost of Rs. 500.
By the given condition, the extra amount cannot exceed Rs. 2,000.
Since this state has been met, we stop with this step.
Result: The following crashing scheme is suggested for the given project:
Reduce the time of E, B and C by one week each.
Project time after crashing is 33 weeks.
Extra amount required = 500 + 1,000 + 500 = Rs. 2,000.
Problem 3
The manager of a company wants to apply crashing for the following project by spending an additional amount not exceeding Rs. 2,000. Offer your suggestion to the manager.

Solution
We have the following network diagram for the given project with normal costs:


Maximum of {70, 62, 69} = 70.
Therefore Path I is the critical path and the critical activities are A, C and F. The non-critical activities are B, D, E and G.
The crash cost per unit time for the activities in the project are provided in the following table

We have to choose one of the activities A, C and F for crashing. The crash cost per unit time is as follows:
Rs. 2,000 for A; Rs. 500 for C; Rs. 1,000 for F.
The least among them is Rs. 500. So we have to choose the activity C for crashing. We reduce the time of C by one week by spending an extra amount of Rs. 500.
After this step, we have the following network with the revised times for the activities:

The time for Path II = 20 + 17 + 25= 62 weeks.
The time for Path III = 15+19 +25 = 69 weeks.
Maximum of {69, 62, 69} = 69.
Since paths I and III have equal times, both are critical paths. So, we can choose an activity for crashing from either of them depending on the least crash cost per unit time.
In path I, the activities are A, C and F. In path III, the activities are B, E and G.
The crash cost per unit time is the least for activity C. So we select C for crashing. Reduce the time of C by one week at an extra cost of Rs. 500.
After this step, we have the following network with the revised times for the activities:

The time for Path II = 20 + 17 + 25= 62 weeks.
The time for Path III = 15+19 +25 = 69 weeks.
Maximum of {68, 62, 69} = 69.
Therefore path III is the critical activities. Hence we have to select an activity from Path III for crashing. We see that the crash cost per unit time is as follows:
Rs. 3,000 for B; Rs. 1,000 for E; Rs. 1,000 for G.
The least among them is Rs. 1,000. So we can select either E or G for crashing. Let us select E for crashing. We reduce the time of E by one week by spending an extra amount of Rs. 1,000.
By the given condition, the extra amount cannot exceed Rs. 2,000.
Since this condition has been reached, we stop with this step.
Result: The following crashing scheme is suggested for the given project: Reduce the time of C by 2 weeks and that of E by one week.
Project time after crashing is 67 weeks.
Extra amount required = 2 x 500 + 1,000 = Rs. 2,000.
Tags : Operations Management - Network Problems
Last 30 days 22650 views












