Research Methodology - Partial And Multiple Correlation
MULTIPLE CORRELATION - Partial And Multiple Correlation
Posted On :
When the value of a variable is influenced by another variable, the relationship between them is a simple correlation.
MULTIPLE CORRELATION

When the value of a variable is influenced by another variable, the relationship between them is a simple correlation. In a real life situation, a variable may be influenced by many other variables. For example, the sales achieved for a product may depend on the income of the consumers, the price, the quality of the product, sales promotion techniques, the channels of distribution, etc. In this case, we have to consider the joint influence of several independent variables on the dependent variable. Multiple correlations arise in this context.
Suppose Y is a dependent variable, which is influenced by n other variables X1, X2, …,Xn. The multiple correlation is a measure of the relationship between Y and X1, X2,…, Xn considered together.
The multiple correlation coefficients are denoted by the letter R. The dependent variable is denoted by X1. The independent variables are denoted by X2, X3, X4,…, etc.
Meaning of notations:
R1.23 denotes the multiple correlation of the dependent variable X1 with two independent variables X 2 and X3 . It is a measure of the relationship that X1 has with X2 and X3 .
R2.13 is the multiple correlation of the dependent variable X2 with two independent variables X1 and X3.
R3.12 is the multiple correlation of the dependent variable X3 with two independent variables X1 and X2.
R1.234 is the multiple correlation of the dependent variable X1 with three independent variables X2 , X3 and X4.
The coefficient of multiple linear correlation is given in terms of the partial correlation coefficients as follows:
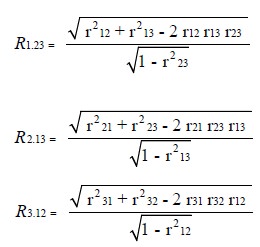
1. The coefficient of multiple linear correlations R is a non-negative quantity. It varies between 0 and 1.


When the value of a variable is influenced by another variable, the relationship between them is a simple correlation. In a real life situation, a variable may be influenced by many other variables. For example, the sales achieved for a product may depend on the income of the consumers, the price, the quality of the product, sales promotion techniques, the channels of distribution, etc. In this case, we have to consider the joint influence of several independent variables on the dependent variable. Multiple correlations arise in this context.
Suppose Y is a dependent variable, which is influenced by n other variables X1, X2, …,Xn. The multiple correlation is a measure of the relationship between Y and X1, X2,…, Xn considered together.
The multiple correlation coefficients are denoted by the letter R. The dependent variable is denoted by X1. The independent variables are denoted by X2, X3, X4,…, etc.
Meaning of notations:
R1.23 denotes the multiple correlation of the dependent variable X1 with two independent variables X 2 and X3 . It is a measure of the relationship that X1 has with X2 and X3 .
R2.13 is the multiple correlation of the dependent variable X2 with two independent variables X1 and X3.
R3.12 is the multiple correlation of the dependent variable X3 with two independent variables X1 and X2.
R1.234 is the multiple correlation of the dependent variable X1 with three independent variables X2 , X3 and X4.
Coefficient Of Multiple Linear Correlations
The coefficient of multiple linear correlation is given in terms of the partial correlation coefficients as follows:
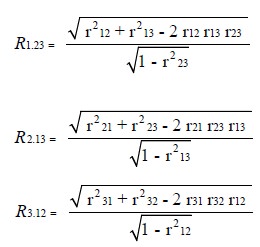
Properties Of The Coefficient Of Multiple Linear Correlations:
1. The coefficient of multiple linear correlations R is a non-negative quantity. It varies between 0 and 1.


Tags : Research Methodology - Partial And Multiple Correlation
Last 30 days 5967 views












