Research Methodology - Factor Analysis And Conjoint Analysis
FACTOR ANALYSIS - Factor Analysis And Conjoint Analysis
Posted On :
In a real life situation, several variables are operating. Some variables may be highly correlated among themselves.
FACTOR ANALYSIS
In a real life situation, several variables are operating. Some variables may be highly correlated among themselves. For example, if manager of a restaurant has to analyse six attributes of a new product. He undertakes a sample survey and finds out the responses of potential consumers. He
The factor analysis is a
multivariate method. It is a statistical technique to identify the underlying
factors among a large number of interdependent variables. It seeks to extract
common factor variances from a given set of observations. It splits a number of
attributes or variables into a smaller group of uncorrelated factors. It
determines which variables belong together. This method is suitable for the
cases with a number of variables having a high degree of correlation.
In the above example, we would like to filter down the attributes 1, 4 into a single attribute. Also we would like to do the same for the attributes 2, 5, 6. If a set of attributes (variables) A1, A2, …, Ak filter down to an attribute Ai (1 ≤ i ≤ k), we say that these attributes are loaded on the factor Ai or saturated with the factor Ai. Sometimes, more than one factor also may be identified.
In a real life situation, several variables are operating. Some variables may be highly correlated among themselves. For example, if manager of a restaurant has to analyse six attributes of a new product. He undertakes a sample survey and finds out the responses of potential consumers. He

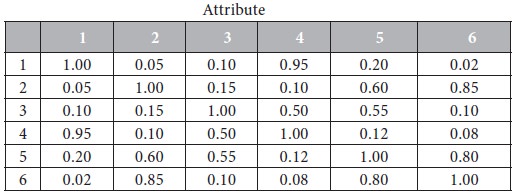
Attribute
Correlation Matrix
We try to group the attributes by their correlations. The high correlation values are observed for the following attributes:
Attributes 1, 4 with a very high correlation coefficient of 0.95.
Attributes 2, 4 with a high correlation coefficient of 0.85.
Attributes 3, 4 with a high correlation coefficient of 0.85.
As a result, it is seen that not all the attributes are independent. The attributes 1 and 4 have mutual influence on each other while the attributes 2, 5 and 6 have mutual influence among themselves. As far as attribute 3 is concerned, it has little correlation with the attributes 1, 2 and 6. Even with the other attributes 4 and 5, its correlation is not high. However, we can say that attribute 3 is somewhat closer to the variables 4 and 5 rather than the attributes 1, 2 and 6. Thus, from the given list of 6 attributes, it is possible to find out 2 or 3 common factors as follows:
We try to group the attributes by their correlations. The high correlation values are observed for the following attributes:
Attributes 1, 4 with a very high correlation coefficient of 0.95.
Attributes 2, 4 with a high correlation coefficient of 0.85.
Attributes 3, 4 with a high correlation coefficient of 0.85.
As a result, it is seen that not all the attributes are independent. The attributes 1 and 4 have mutual influence on each other while the attributes 2, 5 and 6 have mutual influence among themselves. As far as attribute 3 is concerned, it has little correlation with the attributes 1, 2 and 6. Even with the other attributes 4 and 5, its correlation is not high. However, we can say that attribute 3 is somewhat closer to the variables 4 and 5 rather than the attributes 1, 2 and 6. Thus, from the given list of 6 attributes, it is possible to find out 2 or 3 common factors as follows:
I.
1. The common features of the attributes 1,3,4 will give a factor
2. The common features of the attributes 2, 5, 6 will give a factor
Or
II.
1. The common features of the attributes 1,4 will give a factor
2. The common features of the attributes 2,5,6 will give a factor
3. the attribute 3 can be considered to be an independent factor
1. The common features of the attributes 1,3,4 will give a factor
2. The common features of the attributes 2, 5, 6 will give a factor
Or
II.
1. The common features of the attributes 1,4 will give a factor
2. The common features of the attributes 2,5,6 will give a factor
3. the attribute 3 can be considered to be an independent factor
In the above example, we would like to filter down the attributes 1, 4 into a single attribute. Also we would like to do the same for the attributes 2, 5, 6. If a set of attributes (variables) A1, A2, …, Ak filter down to an attribute Ai (1 ≤ i ≤ k), we say that these attributes are loaded on the factor Ai or saturated with the factor Ai. Sometimes, more than one factor also may be identified.
Tags : Research Methodology - Factor Analysis And Conjoint Analysis
Last 30 days 1267 views












