Home | ARTS | Operations Management
|
Model 2 : (M/M/C) : (GD/ ∞/ ∞ ) Model - Types of Waiting Line Models - Queueing Theory
Operations Management - Game Theory, Goal Programming & Queuing Theory
Model 2 : (M/M/C) : (GD/ ∞/ ∞ ) Model - Types of Waiting Line Models - Queueing Theory
Posted On :
The following assumptions are made for this model
Model 2 : (M/M/C) : (GD/ ∞/ ∞ ) Model
The following assumptions are made for this model:
The arrival rate follows Poisson distribution
The service rate follows Poisson distribution
The number of servers is C
The service discipline is general discipline
The maximum number of customers allowed in the system is infinite
With these assumptions, the steady state equation for the probability of having n customers in the system is given by

Example 1
At a Toll Gate, vehicles arrive at the rate of 24 per hour and the arrival rate follows Poisson distribution. The time to collect a toll and permitting the vehicle to pass follows exponential distribution and the passing rate is 18 vehicles per hour. There are 4 passing counters. Determine the following:
1. Po and P3
2. Lq, Ls, Wq and Ws
Solution
The arrival rate δ= 24 per hour.
The passing rate µ = 18 Per hour.
No. of passing counters C=4.


Example 2
In a bank, there are two cashiers in the cash counters. The service time for each customer is exponential with mean 4 minutes and the arrival rate of the customers is 10 per hour and the arrival of the customers follows Poisson distribution. Determine the following:
1. The probability of having to wait for service
2. The expected percentage of idle time for each cashier
3. Whenever a customer has to wait, how much time he is expected to wait in the Bank?
Solution
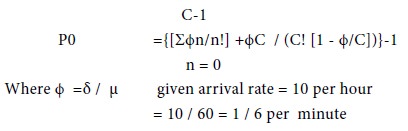

The following assumptions are made for this model:
The arrival rate follows Poisson distribution
The service rate follows Poisson distribution
The number of servers is C
The service discipline is general discipline
The maximum number of customers allowed in the system is infinite
With these assumptions, the steady state equation for the probability of having n customers in the system is given by

Example 1
At a Toll Gate, vehicles arrive at the rate of 24 per hour and the arrival rate follows Poisson distribution. The time to collect a toll and permitting the vehicle to pass follows exponential distribution and the passing rate is 18 vehicles per hour. There are 4 passing counters. Determine the following:
1. Po and P3
2. Lq, Ls, Wq and Ws
Solution
The arrival rate δ= 24 per hour.
The passing rate µ = 18 Per hour.
No. of passing counters C=4.


Example 2
In a bank, there are two cashiers in the cash counters. The service time for each customer is exponential with mean 4 minutes and the arrival rate of the customers is 10 per hour and the arrival of the customers follows Poisson distribution. Determine the following:
1. The probability of having to wait for service
2. The expected percentage of idle time for each cashier
3. Whenever a customer has to wait, how much time he is expected to wait in the Bank?
Solution
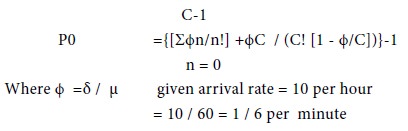

Tags : Operations Management - Game Theory, Goal Programming & Queuing Theory
Last 30 days 2090 views